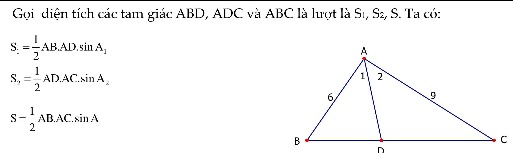
Cho tam giác ABC đường phân giác của góc BAC là AD. Biết AB=6; AC=9 và góc BAC=68. Tính AD

Những câu hỏi liên quan
Cho tam giác ABC đường phân giác của góc BAC là AD. Biết AB=6; AC=9 và góc BAC=68. Tính AD
cho tam giác ABC vs đường phân giác trong của gócBAC là AD bt AB-6 AC=9 cà góc A=68 .Tính độ dài AD
Cho tam giác ABC với đường phân giác trong của góc BAC là AD biết AB=6 AC=9 và góc A=68° tính độ dài AD
Tam giác ABC có AB=2, AC=3. AD là đường phân giác của góc BAC, AD=1,2. Tính góc BAC
Cho tam giác ABC có góc A bằng 120 độ. Kẻ AD là tia phân giác của góc BAC biết AD = AB + AC. CMR: tam giác BCD đều
cho tam giác ABC có góc BAC=120 độ, AB=4cm ,AC=6cm.Tính đường phân giác AD của tam giác ABC
1.Cho tam giác ABC, D là điểm trên AC sao cho AB=CD. Gọi M,N lần lượt là trung điểm của AD, BC. Chúng minh rằng MN song song với phân giác của góc BAC.
2. Cho tam giác ABC, đường phân giác AD, trung tuyến AM. Đường thẳng đi qua D, song song với AB, cắt AM tại I. BI cắt AC tại E. Chứng minh AB=AE.
Bài 1:
Không mất tổng quát giả sử $AB< AC$
Gọi $AH$ là phân giác $\widehat{BAC}$. Theo tính chất tia phân giác:
$\frac{BH}{CH}=\frac{AB}{AC}\Rightarrow \frac{BC}{CH}=\frac{AB+AC}{AC}$
Ta có:
$\frac{HN}{HC}=\frac{BN-BH}{HC}=\frac{BN}{HC}-\frac{BH}{HC}=\frac{BC}{2HC}-\frac{BH}{HC}=\frac{AB+AC}{2AC}-\frac{AB}{AC}$
$=\frac{AC-AB}{2AC}=\frac{AC-CD}{2AC}=\frac{AD}{2AC}=\frac{AM}{AC}$
Theo định lý Talet đảo suy ra $MN\parallel AH$
Ta có đpcm.
Đúng 0
Bình luận (0)
2.
Áp dụng định lý Menelaus với tam giác $AMC$ có $B,I,E$ thẳng hàng ta có:
$\frac{AE}{EC}.\frac{IM}{AI}.\frac{BC}{BM}=1$
$\Leftrightarrow \frac{AE}{EC}=\frac{AI}{2IM}$
$\Rightarrow \frac{AE}{AC}=\frac{AI}{AI+2IM}$
$\Rightarrow \frac{AC}{AE}=\frac{AI+2IM}{AI}(1)$Lại áp dụng tính chất tia phân giác và định lý Talet:
$\frac{AC}{AB}=\frac{CD}{BD}=\frac{CM+DM}{BD}=\frac{BM+DM}{BD}$
$=\frac{BM}{BD}+\frac{DM}{BD}=\frac{AM}{AI}+\frac{IM}{AI}=\frac{AM+IM}{AI}=\frac{AI+2IM}{AI}(2)$
Từ $(1);(2)\Rightarrow \frac{AC}{AB}=\frac{AC}{AE}$
$\Rightarrow AB=AE$ (đpcm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC, AD là tia phân giác góc BAC(D thuộc BC), biết AB=3, AC=4, Bc=6. Tính BD, DC
Cho tam giác ABC ABAC,AD là phân giác của góc BAC D thuộc BC.Trên tia AD lấy điểm M sao cho M nằm giữa A,D a,CM tam giác ABMtam giác ACM và cm tam giác BMC là tam giác cân b,Đường thẳng BM cắt cạnh AC của tam giác ABC tại E,đường thẳng CM cắt cạnh AB của Tam giác ABC tại F.Chứng minh AD vuông góc È c,Trên tia đối của tia CA lấy điểm K(K khác C),đường thẳng BK cắt tia đối của tia DA tại N.Chứng minh KNBN
Đọc tiếp
Cho tam giác ABC AB=AC,AD là phân giác của góc BAC D thuộc BC.Trên tia AD lấy điểm M sao cho M nằm giữa A,D a,CM tam giác ABM=tam giác ACM và cm tam giác BMC là tam giác cân b,Đường thẳng BM cắt cạnh AC của tam giác ABC tại E,đường thẳng CM cắt cạnh AB của Tam giác ABC tại F.Chứng minh AD vuông góc È c,Trên tia đối của tia CA lấy điểm K(K khác C),đường thẳng BK cắt tia đối của tia DA tại N.Chứng minh KN>BN
cho tam giác abc , ad là phân giác của góc bac, biết ab=9, ac=21. tính tỉ số của bd và dc
Cho tam giác ABC có AD là tia phân giác của góc BAC. Biết AB = 3cm, BD = 4cm, CD = 6cm. Tính AC?
A. 4cm
B. 5cm
C. 6cm
D. 4,5cm
Theo tính chất tia phân giác của góc ta có:
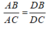
Suy ra:

Chọn đáp án D
Đúng 0
Bình luận (0)