Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?

a) Xét \(\Delta ABC\) vuông tại `A`

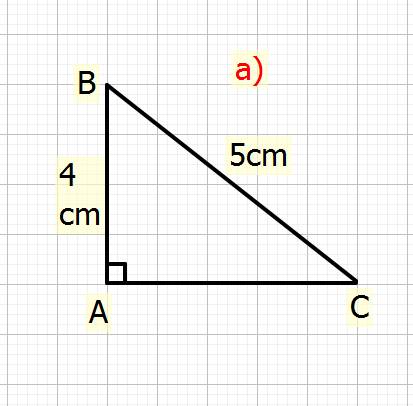
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)

\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\) 

Vậy: \(AC=3cm\)

Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)

\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)

Vậy: Góc C khoảng \(53^o\)

Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)

\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)

Vậy: Góc B khoảng \(37^o\) 

_

b) Xét \(\Delta ABC\) vuông tại `A`

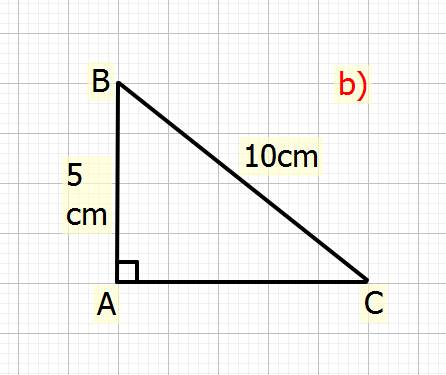
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)

\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)

Vậy: \(AC=5\sqrt{3}cm\)

Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)

 \(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)

Vậy: Góc C là \(30^o\)

Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)

\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)

Vậy: Góc B là \(60^o\).

Áp dụng định lí Pytago có:

\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)

\(\Rightarrow S_{ABC}=\dfrac{AB.AC}{2}=\dfrac{3.4}{2}=6\left(cm^2\right)\)

Diện tích tam giác ABC là:

( 3. 5 ): 2 = 7.5 ( cm²)

Đ/s:...

a) Xét ΔABC có 

\(BC^2=AB^2+AC^2\left(5^2=3^2+4^2\right)\)

nên ΔABC vuông tại A(Định lí Pytago đảo)

Xét ΔABC vuông tại A có 

\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{4}{5}\)
nên \(\widehat{C}\simeq53^0\)

\(\Leftrightarrow\widehat{B}=37^0\)

b) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)

nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)

hay \(\dfrac{BD}{4}=\dfrac{CD}{3}\)

mà BD+CD=5

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{BD}{4}=\dfrac{CD}{3}=\dfrac{BD+CD}{4+3}=\dfrac{5}{7}\)

Do đó: \(BD=\dfrac{20}{7}cm;CD=\dfrac{15}{7}cm\)

13 cm2

đ/l pytago:

AC^2=BC^2-AB^2

=>AC=3cm

SABC=\(\dfrac{AB.AC}{2}=6cm^2\)

Xét \(\Delta ABC\)vuông tại A

=>AB² +AC²=BC²

3²+AC²=5²=> AC²=5²-3²= 25-9=16

=> AC=\(\sqrt{16}\)=4

Diện tích \(\Delta ABC\)  là: (ACxAB)/2=4x3/2=12/2=6(cm²)

Vậy: diện tích am giác ABC là 6 cm²

bạn dùng định lí pitago để tính cạnh AC nhé. AC=căn 34. sau khi có 3 cạnh thì tính diện tích

 Áp dụng định lí Py ta go vào tam giác ABC có:

AC²= BC²-AB²=5²-3²=25-9=16(cm)

=>AC=4(cm)

Diện tích tam giác ABC là:

3.4:2=6(cm)

ĐS:6cm

Chúc bn học giỏi nhoa ~

a: \(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)

\(AD=\dfrac{2\cdot3\cdot4}{3+4}\cdot cos45=\dfrac{12}{7}\sqrt{2}\left(cm\right)\)

b: Sửa đề: vuông góc AC

Xét ΔABC vuông tại A và ΔHDC vuông tại H có

góc C chung

=>ΔABC đồng dạng với ΔHDC

\(1,\)

\(a,\) Áp dụng HTL tam giác

\(\left\{{}\begin{matrix}AH^2=CH\cdot BH\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AH^2}{CH}=\dfrac{25}{6}\left(cm\right)\\AB=\sqrt{\dfrac{25}{6}\left(\dfrac{25}{6}+6\right)}=\dfrac{5\sqrt{61}}{6}\left(cm\right)\\AC=\sqrt{6\left(\dfrac{25}{6}+6\right)}=\sqrt{61}\left(cm\right)\end{matrix}\right.\\ BC=\dfrac{25}{6}+6=\dfrac{61}{6}\left(cm\right)\)

\(b,S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot5\cdot\dfrac{61}{6}=\dfrac{305}{12}\left(cm^2\right)\)