Các câu hỏi tương tự
cho tam giác ABC cân tại A (AB >AC) H là trung điểm của BC. a) Cm rằng :AH là phân giác của BAC b) Tính độ dài AH nếu BC = 4cm ,AB=cm c) Tia phân giác của góc B cắt AH tại M. CM :tam giác BMC cân d) Đường thẳng đi qua A và song song với BC cắt BM tại N. CM :AB=AN e) Kẻ MK vuông góc AC tại K. CM: MH=MK f) CM: MC vuông góc với NC
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H. Biết AB = 20 cm; AH = 16 cm; HC = \(\frac{64}{3}\). Tính chu vi của tam giác ABC.
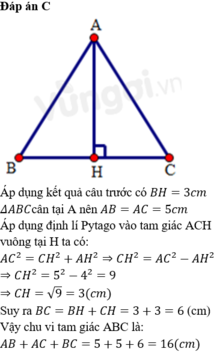
bài 3: Cho tam giác ABC cân tại A có AB = AC = 5cm, BC = 8cm. Gọi H là trung điểm của BC. Tính AH
Bài 4: Cho ABC có AB= 15 cm, AC = 20 cm, BC = 25 cm. Kẻ AH vuông góc với BC tại H. a) Chứng minh: ABC vuông tại A b) Tính diện tích ABC c) Tính AH giúp mik với trình bày rõ cho mik nha
cho tam giác ABC cân tại A. kẻ AH vuông góc BC tại H
a) CM tam giác ABH= tam giác ACH
b) vẽ trung tuyến BM, gọi G là giao điểm của AH và BM. CM G là trọng tâm cuẩ tam giác ABC
c) CHo AB= 30cm, BH= 18 cm. Tính AH<,AG
d) Từ H kẻ HD// với AC ( D thuộc AB) CM 3 điểm C,G,D thẳng hàng
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) Chứng minh tam giác AHB =tam giác AHC
b) AB=10 cm, BC=12 cm. AH = ?
c) HE // AC. E thuộc AB. Cm tam giác AEH cân
d) F là trung điểm AH. CM BF+HE > 3/4 BC
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) Chứng minh tam giác AHB =tam giác AHC
b) AB=10 cm, BC=12 cm. AH = ?
c) HE // AC. E thuộc AB. Cm tam giác AEH cân
d) F là trung điểm AH. CM BF+HE > 3/4 BC
Cho tam giác ABC vuông tại A ( AB<AC) kẻ AH vuông góc với BC , phân giác góc HAC cắt BC tại D
a) Cm : tam giác ABD cân tại B
b) Từ H kẻ đường thẳng vuông góc với AD cắt Ac tại E . CM: DE vuông góc AC
c) Cho AB=15cm, AH=12cm. Tính AD
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) Chứng minh tam giác AHB =tam giác AHC
b) AB=10 cm, BC=12 cm. AH = ?
c) HE // AC. E thuộc AB. Cm tam giác AEH cân
d) F là trung điểm AH. CM BF+HE > 3/4 BC
cho tam giác ABC cân tại A kẻ AH vuông góc với BC (H thuộc BC)
a) chứng minh tam giác ABH = tam giác ABH suy ra AH là tia phân giác của BAC
b) Kẻ HD vuông với AB (D ∈ AB), HE⊥ AC (E ∈ AC).chứng minh ▲HDE cân
c) Nếu cho AB= 29 cm, AH= 20 cm. tính độ dài cạnhp AB?
d) chứng minh BC song song DE
e) nếu cho BAC= 120 độ thì▲ HDE trở thành tam giác gì? vì sao
Cho tam giác ABC cân tại A. Kẻ Ah vuông góc với BC( H thuộc BC)
a) CM: HB=HC
b) CM: Ah là tia phân giacscuar góc BAC
c) Qua B vẽ đường thẳng vuông góc với AB, qua C vẽ đường thẳng vuông góc với AC, hai đường thẳng này cắt nhau ở D. Cm tam giác DBC cân.