cho ΔABC có ∠ABC=90 độ; AB = 6cm ; AC=10cm
a, Tình BC=?
b, Trên tia đối của tia BC lấy m sao cho BM = 8cm. Tính AM
c, Hỏi ΔACM có vuông không? vì sao?
d*, Điểm N thuộc tia AB thỏa mãn ΔNCM vuông tại N. Tính NM?
Cho ΔABC có góc A= 90 độ, BC=10,AC=8,Tính AB?
Theo định lí Pytago ta có
\(BC^2=AB^2+AC^2\\ AB^2=BC^2-AC^2=\sqrt{10^2-8^2}\\ =\sqrt{100-64}=6\)
ΔABC có góc A=90 độ ; AB=5cm; BC=13cm .Tính Ac
tự vẽ hình nhé Gọi E là trung điểm của CD.
Xét tam giác BDC ta có:
M là trung điểm của BC ( gt )
E là trung điểm của CD (cách vẽ)
=> EM là đường trung trực của tam giác BDC.
=> EM // BD => EM // ID ( I thuộc BD )
Xét tam giác AME có:
I là trung điểm của AM (gt)
EM // ID (cmt)
=> D là trung điểm của AE
Xét tam giác AME có:
I là trung điểm của AM (gt)
D là trung điểm của AE (cmt)
=> ID là đường trung bình của tam giác AME.
⇒ID=12ME⇒ID=12ME
Mà ME=12BDME=12BD ( ME là đường trung bình của tam giác BDC )
Nên ID=14BD(1)ID=14BD(1)
Xét tam giác ABC vuông tại A ta có:
BC2 = AB2+AC2 ( Định lý Pitago thuận)
Thay:
132 = 52 + AC2
169 = 25 + AC2 => AC2 = 169 - 25 = 144
=> AC2 = 122
=> AC = 12 (cm)
Ta có: AD = ED ( D là trung điểm của AE )
ED = EC ( E là trung điểm của DC)
=> AD = ED = EC
Mà AD + ED + EC = AC (gt)
Nên: AD + AD + AD = AC
=> 3AD = AC
=> AD = AC/3
Mặt khác AC = 12 cm (cmt)
=> AD = 12/3 = 4 (cm)
Xét tam giác ABD vuông tại A ta có:
BD2 = AB2+AD2 ( định lý Pitago thuận)
BD2 = 52+42
BD2 = 25 + 20
BD2 = 45
=> BD=√45⇒BD=3√5(cm)(2)BD=45⇒BD=35(cm)(2)
Thế (2) vào (1) ta được:
ID=3√54(cm)(3)ID=354(cm)(3)
Ta có:
BI + ID = BD ( I thuộc BD )
=> BI = BD - ID (4)
Thế (2), (3) vào (4) ta được:
BI=3√5−3√54BI=35−354
BI=3√5(1−14)BI=35(1−14)
BI=3√5.34BI=35.34
BI=9√54(cm)
ΔABC có góc A=90 độ ; AB=5cm; BC=13cm .Tính Ac
Áp dụng định lí Py-ta-go vào tam giác ABC vuông tại A, ta có:
\(AB^2+AC^2=BC^2\\ AC^2=BC^2-AB^2\\ AC^2=13^2-5^2\\ AC^2=169-25\\ AC^2=144\\ AC=12\left(cm\right)\)
Cho ΔABC , góc A =90 độ , góc B=60độ .
a, So sánh AD và BD
b, Trên BC lấy D sao cho BD=AB . Qua D dựng đường vuông góc với BC cắt tia đối của AB tại E . Chứng minh : ΔABC=ΔDBE
c, H là giao điểm của AC và ED . Chứng minh : BH là phân giác của góc ABC
d, Qua B vẽ đường thẳng vuông góc AB cắt ED tại K . Chứng minh : ΔHBK đều
b) Xét ΔABC vuông tại A và ΔDBE vuông tại D có
AB=BD(gt)
\(\widehat{ABC}\) chung
Do đó: ΔABC=ΔDBE(cạnh góc vuông-góc nhọn kề)
c) Xét ΔBAH vuông tại A và ΔBDH vuông tại D có
BH chung
BA=BD(gt)
Do đó: ΔBAH=ΔBDH(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{ABH}=\widehat{DBH}\)(hai góc tương ứng)
hay BH là tia phân giác của \(\widehat{ABC}\)
d) Ta có: BH là tia phân giác của \(\widehat{ABC}\)(cmt)
nên \(\widehat{ABH}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)
Ta có: \(\widehat{ABH}+\widehat{HBK}=90^0\)
\(\Leftrightarrow\widehat{HBK}+30^0=90^0\)
hay \(\widehat{HBK}=60^0\)
Xét ΔCHD vuông tại D và ΔCBA vuông tại A có
\(\widehat{ACB}\) chung
Do đó: ΔCHD\(\sim\)ΔCBA(g-g)
Suy ra: \(\widehat{CHD}=\widehat{CBA}\)(hai góc tương ứng)
\(\Leftrightarrow\widehat{CHD}=60^0\)
mà \(\widehat{CHD}=\widehat{HKB}\)(hai góc so le trong, BK//AC)
nên \(\widehat{HKB}=60^0\)
Xét ΔHBK có
\(\widehat{HKB}=60^0\)(cmt)
\(\widehat{HBK}=60^0\)(cmt)
Do đó: ΔHBK đều(Dấu hiệu nhận biết tam giác đều)
Cho Tam Giác ABC , Â = 90 độ, AB = 3cm, AC =4cm. Trên cạnh AB, AC, BC lần lượt lấy trung điểm D,E,F. a) Tìm các cặp cạnh đường thẳng song song? Vì sao? b) Tam giác DFB có đồng dạng với tam giác ECF không? Vì Sao? c) Tính S ΔABC.
Vẽ tam giác ABC có góc A = 90°; AC = 3cm, góc C = 60°. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.
a) Chứng minh ΔABD = ΔABC
b) Tam giác BCD là tam giác gì? Vì sao?
c) Tính độ dài các đoạn thẳng BC, AB
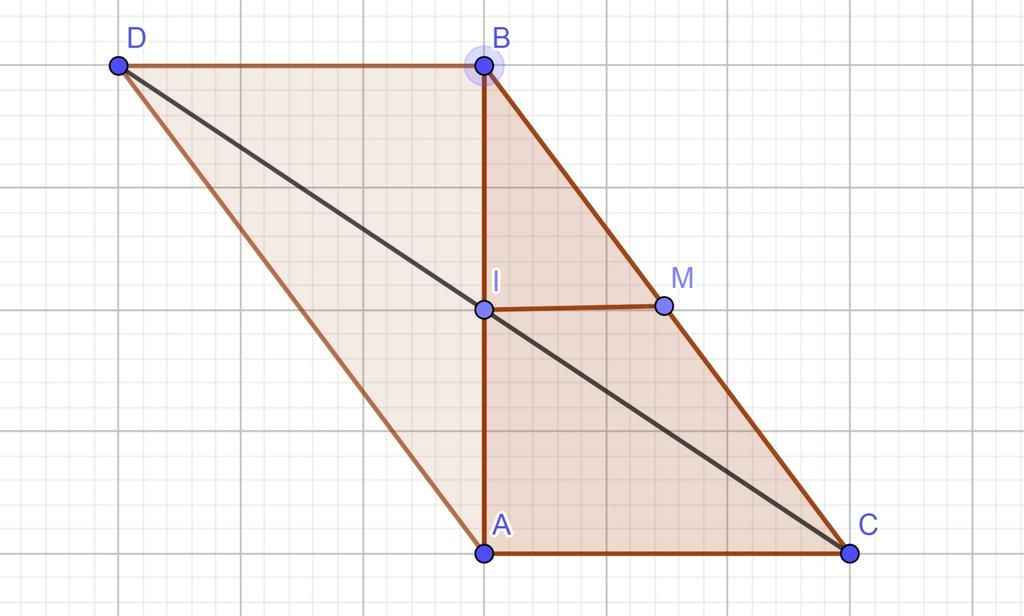
Cho tam giác ABC có A= 90 độ, AC = 5cm, BC = 13cm. Gọi I là trung điểm của cạnh AB, D là điểm đối xứng với C qua I.
a) Tứ giác ADBC là hình gì? Vì sao?
b) Gọi M là trung điểm của cạnh BC. Chứng minh: MI vuông góc với AB. Tính diện tích ΔABC.
a) Xét tứ giác \(ADBC\) ta có :
\(IB=IA\left(g.t\right)\)
\(IC=IC\) ( \(D\) đối xứng qua \(I\))
Vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường
Vậy tứ giác \(ADBC\) là hình bình hành
b) Xét \(\Delta ABC\) ta có :
\(IA=IB\left(g.t\right)\)
\(MB=MC\left(g.t\right)\)
\(\Rightarrow IM\) là đường trung bình \(\Delta ABC\)
Do đó : \(IM\text{/ / }AC\)
Mà \(AB\text{⊥}AC\left(A=90^o\right)\)
Vậy \(IM\text{⊥}AB\)
Áp dụng định lí pytago \(\Delta ABC\) ta có :
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{13^2-5^2}=12\left(cm\right)\)
\(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.13.5=30\left(cm^2\right)\)
Cho ΔABC có A^= 90 độ, vẽ tia phân giác C^ cắt AB ở H. Lấy E ∈BC sao cho CA = CE
a) Chứng minh ΔCAH = ΔCEH và HE ⊥ BC
b) Kẻ EK ⊥ AC tại K, EK cắt CH tại I. Chứng minh ˆHEI = HAI^
c) Chứng minh HE // AI và ˆAIE−ˆABC= 90 độ
Cho ΔABC , góc A =90 độ , AH⊥BC tại H , biết AH =2cm , HB=1cm . Tính HC , AC
Áp dụng hệ thức liên quan tới đường cao vào \(\Delta ABC\), ta có:
\(AH^2=BH.HC\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{2^2}{1}=4\left(cm\right)\)
Mặt khác, áp dụng định lý Pytago vào \(\Delta BHA\), ta có:
\(AB^2=AH^2+BH^2\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{2^2+1}=\sqrt{5}\left(cm\right)\)
Áp dụng hệ thức giữa đường cao và các cạnh vào \(\Delta ABC\), ta có:
\(AB.AC=AH.BC\Rightarrow AC=\dfrac{AH.BC}{AB}=\dfrac{2.\left(1+4\right)}{\sqrt{5}}=2\sqrt{5}\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
nên \(HC=\dfrac{2^2}{1}=4\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AC^2=HC\cdot BC\)
nên \(AC^2=20\)
hay \(AC=2\sqrt{5}\left(cm\right)\)