Tìm GTNN của biểu thức;
A=(X-1)(X-3)+11
Những câu hỏi liên quan
1. cho x+y = 1 . tìm GTNN của biểu thức C = x2 + y2
2. cho x + 2y =1 . tìm GTNN của biểu thức P = x2 + 2y2
3. cho x + y =1 . tìm GTNN của biểu thức G = 2x2 + y2
4. cho x + y =1 . tìm GTNN của biểu thức H = x2 + 3y2
5. cho 2x + y =1 . tìm GTNN của biểu thức I = 4x2 + 2y2
6. tìm các số thực thõa mãn Pt :
2x2 + 5y2 + 8x - 10y + 13 = 0
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
Đúng 1
Bình luận (0)
a) Tìm GTNN của biểu thức A = x2 - 2x +5
b) Tìm GTNN của biểu thức B = 2x2 - 6x
c) Tìm GTNN của biểu thức C = 4x - x2 = 3
a) x2 - 2x + 5 = (x - 1)2 + 4 >= 4
Min là 4 khi x = 1
Đúng 0
Bình luận (0)
Cho
x
,
y
∈
ℤ
a) Với giá trị nào của x thì biểu thức
A
1000
−
x
+
5
có GTLN; Tìm GTLN đó. b) Với giá trị nào của y thì biểu thức
B
y
−
3
+
50
có GTNN. Tìm GTNN đó. c) Với giá trị nào của x, y thì biểu thức ...
Đọc tiếp
Cho x , y ∈ ℤ
a) Với giá trị nào của x thì biểu thức A = 1000 − x + 5 có GTLN; Tìm GTLN đó.
b) Với giá trị nào của y thì biểu thức B = y − 3 + 50 có GTNN. Tìm GTNN đó.
c) Với giá trị nào của x, y thì biểu thức C = x − 100 + y + 200 − 1
có GTNN. Tìm GTNN đó
Cho x,y thuộc Z :
a/ Với giá trị nào của x thì biểu thức của A=2006-|x+5|có GTLN?Tìm GTLN đó?
b/Với giá trị nào của y thì biểu thức của B=|y-3|-9 có GTNN ?Tìm GTNN đó?
c/Tìm GTNN của biểu thức C=|x-100|+|y+200|-1?
GTNN là gì z.tui ko hiểu nên ko giải được!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) Tìm GTNN của biểu thức: a − 7 + 12
b) Tìm GTLN của biểu thức: 2017 − x + 3
Cho x,y thuộc Z:
a)Với giá trị nào của x thì biểu thức A=1000- |x+5| có GTLN;tìm GTLN đó.
b)Với giá trị nào của y thì biểu thức B=|y-3|+50 có GTNN;tìm GTNN đó.
c)Với giá trị nào của x và y thì biểu thức C=|x-100| +|y+200| -1 có GTNN;tìm GTNN đó.
Tìm GTNN của biểu thức C= x+2020/(x+2021)^2 *biểu thức C là phân thức
Tìm GTNN của biểu thức:
Đọc tiếp
Tìm GTNN của biểu thức:
\(A=\sqrt{x-1}+\sqrt{2}\ge\sqrt{2}\\ A_{max}=\sqrt{2}\Leftrightarrow x-1=0\Leftrightarrow x=1\)
Đúng 0
Bình luận (0)
\(A=\sqrt{x-1}+\sqrt{2}\ge\sqrt{2}\forall x\)
Dấu '=' xảy ra khi x=1
Đúng 0
Bình luận (0)
16 tháng 7 2023 lúc 16:16
Tìm GTNN của biểu thức
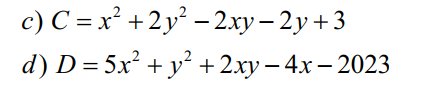
c) C = x2 - 2xy+ y2 + y^2 - 2y +1 +2
= (x-y)^2 + (y - 1)^2 + 2
Ta có (x-y)^2;(y-1)^2 lớn hơn hoặc bằng 2
Dấu "=" xảy ra => (y-1)^2 = 0 => y-1=0 => y = 1
(x-y)^2 = 0 => x - y = 0 => x - 1= 0 => x = 1
d) D = \(4x^2-4x+1+x^2+2xy+y^2-2024\)
= \(\left(2x-1\right)^2+\left(x+y\right)^2-2024\)
Ta có (2x-1)^2;(x+y)^2 ≥ 0 => D ≥ -2024
Dấu = xảy ra => (2x-1)^2 = 0 => 2x-1 = 0 => x = 1/2
=> (x+y)^2 =0 => x+y=0 => 1/2+y =0 => y = -1/2
Đúng 1
Bình luận (0)
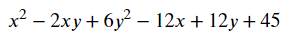
Tìm GTNN của biểu thức
\(=\left(x^2-2xy+y^2\right)-12\left(x-y\right)+36+5y^2+9\)
\(=\left(x-y\right)^2-12\left(x-y\right)+36+3y^2+9\)
\(=\left(x-y-6\right)^2+5y^2+9\ge9\)
Vậy GTNN của biểu thức là 9, xảy ra khi \(x=6;y=0\)
Đúng 3
Bình luận (0)