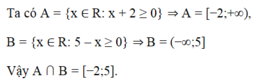Cho R\{ 0 ; 2 ; 4 } có phải là tập xác định của hàm số y = 2-x / x^2 - 4x

Những câu hỏi liên quan
Cho r là số dư trong phép chia a cho b ( với b ≠ 0 ), khi đó:
A. r = b B. r > b
C. r > 0 D. 0 ≤ r < b
Xem thêm câu trả lời
Cho các đa thức f(x),�(�), g(x)�(�) và h(x).ℎ(�). Xét các tập hợp X{x∈R|f(x)0},�{�∈�|�(�)0}, Y{x∈R|g(x)0},�{�∈�|�(�)0}, Z{x∈R|h(x)0}�{�∈�|ℎ(�)0} và T{x∈R|f2(x)+|g(x)|+√h(x)≤0}.�{�∈�|�2(�)+|�(�)|+ℎ(�)≤0}. Trong các mệnh đề dưới đây, mệnh đề nào đúng ?A. TX∪Y∪Z.��∪�∪�.B. TX∩Y∩Z.��∩�∩�.C. TX
Đọc tiếp
Cho các đa thức và Xét các tập hợp và Trong các mệnh đề dưới đây, mệnh đề nào đúng ?
A.
B.
C.
1. Cho Q = \(\frac{ab}{c}\). Với giá trị nào của các chữ thì:
a) R = 0; b) R > 0; c) R < 0 ?
2. Cho R = \(\frac{a^2b}{c}\). Với giá trị nào của các chữ thì:
a) R = 0; b) R > 0; c) R < 0 ?
Nhớ giải thích rõ ràng, chi tiết.
Các bạn ơi câu 1 là Q ko phải R mình viết lộn câu 2
Đúng 0
Bình luận (0)
cho đường tròn(0;R) và đường tròn(0';r) (R>r) tiếp xúc ngoài tại A .Vẽ tiếp tuyến chung ngoài BC.(B thuộc (0);C thuộc (0') ).Tiếp tuyến chung ngoài tại A cắt BC tại I. Chứng minh IH.IO + IK.IO' =2Rr
Cho các tập hợp A {x ∈ R : (x2 - 4) (x2 - 1) 0}; B {x ∈ R : (x2 - 4) (x2 + 1) 0}; C {-1; 0; 1; 2}; D {x ∈ R :
x
4
-
5
x
2
+
4
x
0}. Khẳng định nào sau đây đúng? A. A B. B. C A. C. D B. D. D A.
Đọc tiếp
Cho các tập hợp A = {x ∈ R : (x2 - 4) (x2 - 1) = 0}; B = {x ∈ R : (x2 - 4) (x2 + 1) = 0}; C = {-1; 0; 1; 2}; D = {x ∈ R : x 4 - 5 x 2 + 4 x = 0}. Khẳng định nào sau đây đúng?
A. A = B.
B. C = A.
C. D = B.
D. D = A.
Đáp án: D
(x2 - 4) (x2 - 1) = 0 ⇔ x = ±2; x = ±1 nên A = {-2; -1; 1; 2}
(x2 - 4) (x2 + 1) = 0 ⇔ x2 - 4 = 0 ⇔ x = ±2 nên B = {-2; 2}
x4 - 5x2 + 4)/x = 0 ⇔ x4 - 5x2 + 4 = 0 ⇔ x = ±2; x = ±1 nên D = {-2; -1; 1; 2}
=> A = D
Đúng 0
Bình luận (0)
Cho hai tập hợp E {x ∈ R: f(x) 0}; F { x ∈ R: g(x) 0}; H {x ∈ R:
f
(
x
)
g
(
x
)
0}. Trong các mệnh đề sau, mệnh đề đúng là: A. H E ∪ F. B. H E ∩ F. C. H E F. D. H F E.
Đọc tiếp
Cho hai tập hợp E = {x ∈ R: f(x) = 0}; F = { x ∈ R: g(x) = 0}; H = {x ∈ R: f ( x ) g ( x ) = 0}. Trong các mệnh đề sau, mệnh đề đúng là:
A. H = E ∪ F.
B. H = E ∩ F.
C. H = E \ F.
D. H = F \ E.
Đáp án: C
f(x)/g(x) = 0 ⇔ f(x) = 0 và g(x) ≠ 0. Nghĩa là H là tập hợp bao gồm các phần tử thuộc E nhưng không thuộc F hay H = E \ F.
Đúng 0
Bình luận (0)
Cho hai tập hợp E {x ∈ R: f(x) 0}; F { x ∈ R: g(x) 0}; H {x ∈ R : f(x).g(x) 0}. Trong các mệnh đề sau, mệnh đề đúng là: A. H E ∪ F. B. H E ∩ F. C. H E F. D. H F E.
Đọc tiếp
Cho hai tập hợp E = {x ∈ R: f(x) = 0}; F = { x ∈ R: g(x) = 0}; H = {x ∈ R : f(x).g(x) = 0}. Trong các mệnh đề sau, mệnh đề đúng là:
A. H = E ∪ F.
B. H = E ∩ F.
C. H = E \ F.
D. H = F \ E.
Đáp án: A
f(x).g(x) = 0 ⇔ f(x) = 0 hoặc g(x) = 0. Nghĩa là H là tập hợp bao gồm các phần tử thuộc E hoặc thuộc F hay H = E ∪ F.
Đúng 0
Bình luận (0)
Cho (P): 2x + y – 4 = 0 và (Q): 3y + z +2 = 0 cắt nhau theo giao tuyến là đường thẳng d. Viết ptmp(R) biết
a) (R) vuông góc với d và qua O(0; 0; 0)
b) (R) chứa d và qua M(1;-1;3)
c) (R) chứa d và qua N(7;-1;1)
d) (R) chứa d và song song với AB biết (-1; 1; 0) và B(2; -1; 2)
Cho hai tập hợp E {x ∈ R: f(x) 0}; F {x ∈ R: g(x) 0}; H { x ∈ R: f(x)2 + g(x)2 0}. Trong các mệnh đề sau, mệnh đề đúng là A. H E ∪ F. B. H E ∩ F. C. H E F. D. H F E.
Đọc tiếp
Cho hai tập hợp E = {x ∈ R: f(x) = 0}; F = {x ∈ R: g(x) = 0}; H = { x ∈ R: f(x)2 + g(x)2 = 0}. Trong các mệnh đề sau, mệnh đề đúng là
A. H = E ∪ F.
B. H = E ∩ F.
C. H = E \ F.
D. H = F \ E.
Đáp án: B
f(x)2 + g(x)2 = 0 ⇔ f(x) = 0 và g(x) = 0. Nghĩa là H là tập hợp bao gồm các phần tử vừa thuộc E vừa thuộc F hay H = E ∩ F
Đúng 0
Bình luận (0)
Cho A = {x ∈ R: x + 2 ≥ 0}, B = {x ∈ R: 5 – x ≥ 0}. Khi đó A ∩ B là
A. [−2;5].
B. [−2;6].
C. [−5;2].
D. (−2;+ ∞ ).