Giúp mình câu này với huhu:((( Câu 57: Tam giác ABC có A(3; - 1) , B(6; 2) , C(1; 4) và đường cao AH . Phương trình đường thẳng AH là 5x + by + c = 0 . Khi đó b + c bằng ...

Những câu hỏi liên quan
Cho tam giác ABC có AB3/4(AB+AC+BC) Ai giúp mình câu này nhanh với ạ😭
Cho tam giác ABC vuông tại A có AH là đường caoa. c/m tam giác HBA đồng dạng tam giác ABC và AB.AB BH.BC ( câu này mình làm rồi)b. chứng minh: HA. HA HB . HC ( câu này mình cũng làm rồi)c. Đường phân giác của góc AHB cắt AB tại E và đường phân giác của góc AHC cắt AC tại F. Chứng minh HA.HF HC. HEd. C/m tam giác HEF đồng dạng tam giác ABCChỉ mình câu c với câu d với mọi người
Đọc tiếp
Cho tam giác ABC vuông tại A có AH là đường cao
a. c/m tam giác HBA đồng dạng tam giác ABC và AB.AB = BH.BC ( câu này mình làm rồi)
b. chứng minh: HA. HA = HB . HC ( câu này mình cũng làm rồi)
c. Đường phân giác của góc AHB cắt AB tại E và đường phân giác của góc AHC cắt AC tại F. Chứng minh HA.HF = HC. HE
d. C/m tam giác HEF đồng dạng tam giác ABC
Chỉ mình câu c với câu d với mọi người
Mọi người giúp mình câu này nhé! ;)Bài duy nhất: Cho tam giác ABC vuông tại A.Tia phân giác của góc B cắt cạnh AC tại E.Từ E kẻ EH vuông góc với BC tại H.CMR:a)Tam giác ABETam giác HBE (mình làm đc rồi)b)BE là đường trung trực của AH (mình cũng làm xong rồi)c)Gọi giao điểm của AB và EH là K.Chứng minh rằng EKEC (hix,con này mình chưa làm đc nè huhu) Mong mọi người giúp đỡ!Mình xin cảm ơn và chúc các bạn năm mới vui vẻ,mạnh khỏe và hạnh phúc nhé! 3
Đọc tiếp
Mọi người giúp mình câu này nhé! ;)
Bài duy nhất: Cho tam giác ABC vuông tại A.Tia phân giác của góc B cắt cạnh AC tại E.Từ E kẻ EH vuông góc với BC tại H.CMR:
a)Tam giác ABE=Tam giác HBE (mình làm đc rồi)
b)BE là đường trung trực của AH (mình cũng làm xong rồi)
c)Gọi giao điểm của AB và EH là K.Chứng minh rằng EK=EC (hix,con này mình chưa làm đc nè huhu)
Mong mọi người giúp đỡ!Mình xin cảm ơn và chúc các bạn năm mới vui vẻ,mạnh khỏe và hạnh phúc nhé! <3
Mọi người ơi giúp mình với, không biết câu này có ra không nhỉ: Cho tam giác ABC. M là trung điểm AB, N thuộc AC sao cho AN = 2/3 AC. Tính tỉ số diện tích tam giác: SABC/SAMN
\(\dfrac{S_{ABC}}{S_{AMN}}=\dfrac{\dfrac{1}{2}AB.AC.sinA}{\dfrac{1}{2}AM.AN.sinA}=\dfrac{AB.AC}{\dfrac{1}{2}AB.\dfrac{2}{3}AC}=3\)
Đúng 1
Bình luận (2)
\(AN=\dfrac{2}{3}AC\Rightarrow CN=\dfrac{1}{3}AC\)
\(\dfrac{S_{CBN}}{S_{ABC}}=\dfrac{\dfrac{1}{2}CN.CB.sinC}{\dfrac{1}{2}CA.CB.sinC}=\dfrac{\dfrac{1}{3}CA}{CA}=\dfrac{2}{3}\)
\(S_{ABC}=S_{AMN}+S_{BNM}+S_{CBN}\)
\(\Rightarrow S_{BMN}=S_{ABC}-S_{AMN}-S_{CBN}=S_{ABC}-\dfrac{1}{3}S_{ABC}-\dfrac{1}{3}S_{ABC}=\dfrac{1}{3}S_{ABC}\)
\(\Rightarrow\dfrac{S_{ABC}}{S_{BMN}}=3\)
Đúng 1
Bình luận (1)
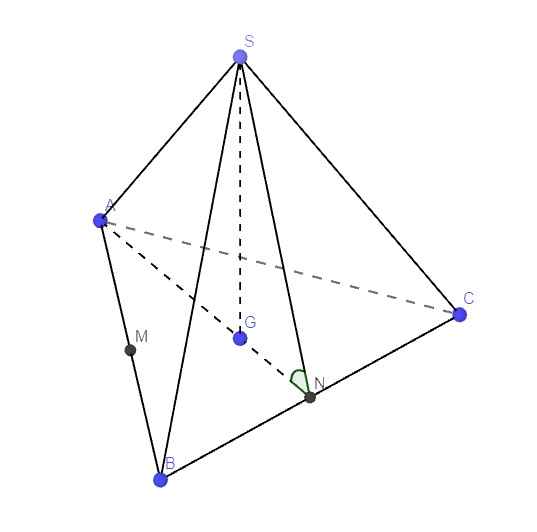
Cho hình chóp tam giác đều S.ABC có M.N lần lượt là trung điểm AB, BC. Biết AB = 2a , SA = (a * sqrt(21))/3 tính góc giữa hai mặt phẳng (SBC) và (ABC) . Giúp mình câu này với
Gọi G là trọng tâm ABC \(\Rightarrow SG\perp\left(ABC\right)\) do S.ABC là chóp đều
\(\Rightarrow SG\perp BC\)
Mà \(AN\perp BC\) (do tam giác ABC đều)
\(\Rightarrow BC\perp\left(SAN\right)\)
\(\Rightarrow\widehat{SNA}\) là góc giữa (ABC) và (SBC)
\(AN=\dfrac{AB.\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)
\(AG=\dfrac{2}{3}AN=\dfrac{2a\sqrt{3}}{3}\) ; \(GN=\dfrac{1}{3}AN=\dfrac{a\sqrt{3}}{3}\) (t/c trọng tâm)
\(SG=\sqrt{SA^2-AG^2}=a\)
\(\Rightarrow tan\widehat{SNA}=\dfrac{SG}{GN}=\sqrt{3}\Rightarrow\widehat{SNA}=60^0\)
Đúng 1
Bình luận (0)
Giải giúp mình với...mình thử giải rồi mà đáp án sợ sai!
Câu 1 :
Cho tam giác ABC có góc A = 105 độ; góc B = 45 độ;BC = 4cm. Tính AB AC?
Câu 2 :
Cho tam giác ABC có góc A = 60 độ; AB =28cm; AC = 35cm. Tính BC
Câu 3:
Cho tâm giác ABC có AB=25cm; góc B=70 độ; góc C=50 độ. Tính BC
-Ai rảnh thì kẻ hình giúp mình luôn nha <3
Giải giúp mình với...mình thử giải rồi mà đáp án sợ sai!
Câu 1 :
Cho tam giác ABC có góc A = 105 độ; góc B = 45 độ;BC = 4cm. Tính AB AC?
Câu 2 :
Cho tam giác ABC có góc A = 60 độ; AB =28cm; AC = 35cm. Tính BC
Câu 3:
Cho tâm giác ABC có AB=25cm; góc B=70 độ; góc C=50 độ. Tính BC
-Ai rảnh thì kẻ hình giúp mình luôn nha <3
ABH^ = 45* và AHB^ = 90* => AHB là tam giác vuông cân
=> AH = BH (1)
ACH^ = 180* - A^ - B^ = 180* - 105* - 45* = 30*
=> AH = AC/2 => AC = 2AH
BC = CH + BH = 4 => CH = 4 - BH (2)
(1) và (2) => CH = 4 - AH
AC^2 = CH^2 + AH^2
4AH^2 = (4 - AH)^2 + AH^2
4AH^2 = 16 - 8AH^2 + AH^2 + AH^2
<=> 2AH^2 + 8AH - 16 = 0
<=> AH^2 + 4AH - 8 = 0
=> AH = 2(√3 -1)
=> AB^2 = 2AH^2 = 2.4(3 - 2√3 + 1) = 8(4 - 2√3) = 16(2 - √3)
=> AB = 4√(2 - √3)
AC = 2AH = 4(√3 -1)
Đúng 1
Bình luận (0)
bạn nên nhớ 2 công thức sau:
+ trong tam giác có góc A = 60độ thì ta có: BC² = AB² + AC² - AC.AB.
+ trong tam giác có góc A = 120độ thì ta có: BC² = AB² + AC² + AC.AB.
Giải: Kẻ đường cao BH của ∆ABC. xét tam giác ABH vuông tại H, có góc BAH = 60độ => góc ABH = 30độ => AB = 2.AH (bổ đề: trong tam giác vuông có góc = 30độ, thì cạnh đối diện với góc 30độ = nửa cạnh huyền - c/m không khó)..
Xét ∆BHC vuông tại H => BC² = BH² + HC² = BH² + (AC - AH)²
= BH² + AH² + AC² - 2.AH.AC
= (BH² + AH²) + AC² - AB.AC (vì AB = 2AH)
= AB² + AC² - AB.AC => ta đã c/m đc. công thức 1. Thay AB = 28cm và AC = 35cm vào ta tính được BC = √1029 (cm) ≈ 32,08 (cm)
Công thức 2 thì cách chứng minh cũng khá giống, cũng kẻ đường cao từ B. Tự chứng minh nha bạn ^^
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải giúp mình với...mình thử giải rồi mà đáp án sợ sai!
Câu 1 :
Cho tam giác ABC có góc A = 105 độ; góc B = 45 độ;BC = 4cm. Tính AB AC?
Câu 2 :
Cho tam giác ABC có góc A = 60 độ; AB =28cm; AC = 35cm. Tính BC
Câu 3:
Cho tâm giác ABC có AB=25cm; góc B=70 độ; góc C=50 độ. Tính BC
-Ai rảnh thì kẻ hình giúp mình luôn nha <3
Giải giúp mình với...mình thử giải rồi mà đáp án sợ sai!
Câu 1 :
Cho tam giác ABC có góc A = 105 độ; góc B = 45 độ;BC = 4cm. Tính AB AC?
Câu 2 :
Cho tam giác ABC có góc A = 60 độ; AB =28cm; AC = 35cm. Tính BC
Câu 3:
Cho tâm giác ABC có AB=25cm; góc B=70 độ; góc C=50 độ. Tính BC
-Ai rảnh thì kẻ hình giúp mình luôn nha <3