Question

Cho hình chóp tam giác đều S.ABC có M.N lần lượt là trung điểm AB, BC. Biết AB = 2a , SA = (a * sqrt(21))/3 tính góc giữa hai mặt phẳng (SBC) và (ABC) . Giúp mình câu này với

Answer 1

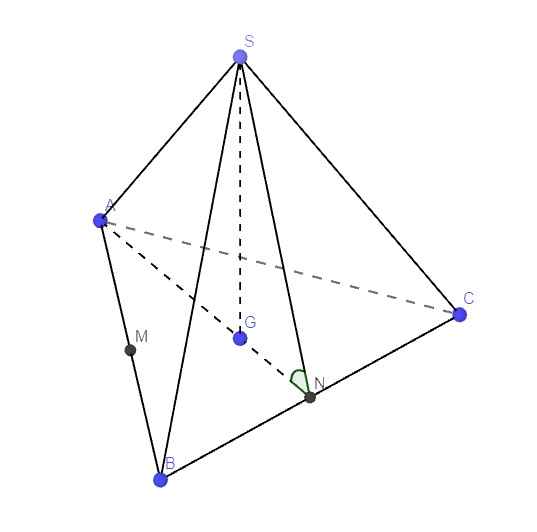
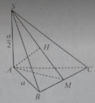
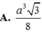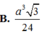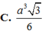Gọi G là trọng tâm ABC \(\Rightarrow SG\perp\left(ABC\right)\) do S.ABC là chóp đều

\(\Rightarrow SG\perp BC\)

Mà \(AN\perp BC\) (do tam giác ABC đều)

\(\Rightarrow BC\perp\left(SAN\right)\)

\(\Rightarrow\widehat{SNA}\) là góc giữa (ABC) và (SBC)

\(AN=\dfrac{AB.\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)

\(AG=\dfrac{2}{3}AN=\dfrac{2a\sqrt{3}}{3}\) ; \(GN=\dfrac{1}{3}AN=\dfrac{a\sqrt{3}}{3}\) (t/c trọng tâm)

\(SG=\sqrt{SA^2-AG^2}=a\)

\(\Rightarrow tan\widehat{SNA}=\dfrac{SG}{GN}=\sqrt{3}\Rightarrow\widehat{SNA}=60^0\)

Answer 2