y = x 2 + 2 x + m - 4 = ( x + 1 ) 2 + m - 5

Ta có  ( x + 1 ) 2 + m - 5 ∈ m - 5 ; m - 1

Giá trị lớn nhất của hàm số   y = x 2 + 2 x + m - 4 trên đoạn[ -2; 1] đạt giá trị nhỏ nhất khi

  m - 5 < 0 m - 1 > 0 5 - m = m - 1 ⇔ m = 3

Chọn B.

Chọn C.

+ Xét hàm số f(x) =x²- 2x  trên đoạn [ -1; 2],

+  ta có đạo hàm f’(x) = 2( x-1)  và f’( x) =0 khi x= 1  

Vậy: 

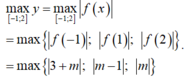
TH1: Với  m a x [ - 1 , 2 ]   =   | m - 1 | ,

ta có  m - 1   ≥ m + 3 | m - 1 |   ≥ | m | | m - 1 |   =   5  

↔ | m - 1 | ≥ m + 3 | m - 1 |   ≥ | m | m   =   - 4   ∨   m   =   6 ↔ m   =   - 4

TH2: Với

  m a x [ - 1 , 2 ]   y   =   | m + 3 |   ↔ | m + 3 |   ≥ | m - 1 | | m + 3 |   ≥ | m | | m + 3 |   ≥ 5

  ↔ | m + 3 |     ≥ |   | m - 1 | | m + 3 |   ≥ | m | m   =   2   ∨   m   =   - 8   ↔   m   =   2

TH3: Với

  m a x     [ - 1 , 2 ]       y   =   | m |   ↔ | m | ≥ | m - 1 | | m | ≥ | m + 3 | | m |   =   5 ↔   | m |   ≥ | m - 1 | | m | ≥ | m + 3 | m   =   5   ∨   m   =   - 5

( vô nghiệm)

Chọn D.

Chọn D

Điều kiện: x  ≠ m

Hàm số đã cho xác định trên [0;4] khi 

Ta có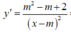 

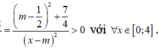
Hàm số đồng biến trên đoạn [0;4] nên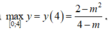 

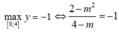
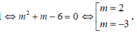
Kết hợp với điều kiện (*) ta được m = -3. Do đó có một giá trị của m thỏa yêu cầu bài toán.

\(y=\left|x^2-2x-m\right|=-x^2+2x+m\)

\(\left(nếu:x^2-2x-m< 0\right)\)

\(f\left(x\right)=-x^2+2x+m\Rightarrow x=\dfrac{-b}{2a}=1\in\left[-3;2\right]\)

\(f\left(-3\right)=m-15\)

\(f\left(1\right)=m+1\)

\(f\left(2\right)=m\Rightarrow f\left(-3\right)< f\left(2\right)< f\left(1\right)\)

\(\Rightarrow max_{f\left(x\right)}=m+1=10\Leftrightarrow m=9\)

\(do..m< 0\Rightarrow m=9\left(ktm\right)\)

\(\Rightarrow không\) \(có\) \(giá\) \(trị\) \(m\) \(thỏa\)