Trong không gian Oxyz. Tính thể tích V của khối đa diện giới hạn bởi mặt phẳng (P) ; 2x-4y+3z-24=0 và các mặt phẳng tọa độ.
A. V=576
B. V=288
C. V=192
D. V=96
Những câu hỏi liên quan
Trong không gian Oxyz. Tính thể tích V của khối đa diện giới hạn bởi mặt phẳng (P): 2x - 4y + 3z - 24 0 và các mặt phẳng tọa độ. A. V 576 B. V 288 C. V 192 D. V 96
Đọc tiếp
Trong không gian Oxyz. Tính thể tích V của khối đa diện giới hạn bởi
mặt phẳng (P): 2x - 4y + 3z - 24 = 0 và các mặt phẳng tọa độ.
A. V = 576
B. V= 288
C. V = 192
D. V = 96
Đáp án D
Ta có:
2 x - 4 y + 3 z - 24 = 0 ⇔ x 12 - y 6 + z 8 = 1
Do đó mặt phẳng (P) cắt các trục Ox; Oy; Oz lần lượt tại các điểm A(12; 0;0); B(0;-6;0); C(0;0;8). Khối đa diện cần tính thể tích là khối tứ diện OABC có OA, OB, OC đôi một vuông góc có độ dài OA=12; OB=6; OC=8
Do đó : V = 1 6 O A . O B . O C = 96 . Chọn D.
Đúng 0
Bình luận (0)
Trong không gian (Oxyz), cho vật thể (H) giới hạn bởi hai mặt phẳng có phương trình x a và x b (
b
a
) Gọi S(x) là diện tích thiết diện của (H) bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x, với
a
≤
x
≤
b
.
Giả sử hàm số
y
S
(
x
)
liên tục trên đoạn [a;b]. Khi đó, thể tích V của vật thể (H) được cho b...
Đọc tiếp
Trong không gian (Oxyz), cho vật thể (H) giới hạn bởi hai mặt phẳng có phương trình x = a và x = b ( b < a ) Gọi S(x) là diện tích thiết diện của (H) bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x, với a ≤ x ≤ b . Giả sử hàm số y = S ( x ) liên tục trên đoạn [a;b]. Khi đó, thể tích V của vật thể (H) được cho bởi công thức:
A. V = π ∫ a b S ( x ) 2 d x
B. V = π ∫ a b S ( x ) d x
C. V = ∫ a b S ( x ) 2 d x
D. V = ∫ a b S ( x ) d x
Trong không gian (Oxyz), cho vật thể (H) giới hạn bởi hai mặt phẳng có phương trình xa và xb (ba) Gọi S(x) là diện tích thiết diện của (H) bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x, với
a
≤
x
≤
b
Giả sử hàm số yS(x) liên tục trên đoạn [a;b]. Khi đó, thể tích V của vật thể (H) được cho bởi công thức:
Đọc tiếp
Trong không gian (Oxyz), cho vật thể (H) giới hạn bởi hai mặt phẳng có phương trình x=a và x=b (b<a) Gọi S(x) là diện tích thiết diện của (H) bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x, với a ≤ x ≤ b Giả sử hàm số y=S(x) liên tục trên đoạn [a;b]. Khi đó, thể tích V của vật thể (H) được cho bởi công thức:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
∆
đi qua gốc tọa độ O và điểm I(0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng
∆
một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S. A.
36
2
π
B.
18
π
C.
36
π...
Đọc tiếp
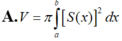
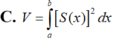
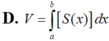
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ đi qua gốc tọa độ O và điểm I(0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng ∆ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S.
A. 36 2 π
B. 18 π
C. 36 π
D. 18 2 π
Đáp án A
Phương pháp:
Tính khoảng cách từ 1 điểm M đến đường thẳng
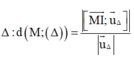
là 1 điểm bất kì
Cách giải:
là một VTCP
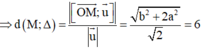
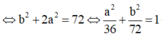
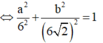
Như vậy tập hợp các điểm M là elip có phương trình
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S. A. 36π B. 36
2
π C. 18
2
π D. 18 π
Đọc tiếp
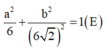
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S.
A. 36π
B. 36 2 π
C. 18 2 π
D. 18 π
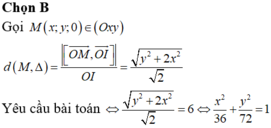
Vậy quỹ tích M trên (Oxy) là hình Elip với
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I(0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S A.
36
2
π
B.
18
π
C.
36
π
D.
18...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I(0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S
A. 36 2 π
B. 18 π
C. 36 π
D. 18 2 π
Đáp án A
Phương pháp:
Tính khoảng cách từ 1 điểm M đến đường thẳng Δ: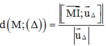 
với
u
△
→
là 1 VTCP của Δ và I
∈
Δ là 1 điểm bất kì
Cách giải: Đường thẳng Δ nhận 
là 1 VTCP
Gọi M(a;b;0)
∈
(Oxy) =>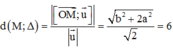 
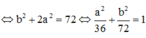
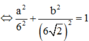
Như vậy tập hợp các điểm M là elip có phương trình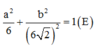 
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hình chóp có đỉnh S ( 2 ; 3 ; 5 ) và đáy là một đa giác nằm trong mặt phẳng (P): 2 x + y - 2 z - 3 = 0 , có diện tích bằng 12. Tính thể tích của khối chóp đó.
A. 4
B. 24
C. 8
D. 72
Đáp án C.
Chiều cao của khối chóp có độ dài bằng d S , P = 2 .
Suy ra thể tích khối chóp đã cho là V = 1 3 . 12 . 2 = 8 .
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hình chóp có đỉnh S(2;3;5) và đáy là một đa giác nằm trong mặt phẳng P : 2 x + y − 2 z − 3 = 0 , có diện tích bằng 12. Tính thể tích của khối chóp đó.
A. 4
B. 24
C. 8
D. 72
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0; 1; 1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S. A. 36π B.
36
2
π
C.
18
2
π
D. 18π
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0; 1; 1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S.
A. 36π
B.
36
2
π
C. 18 2 π
D. 18π
