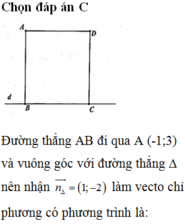
tìm hai số thực dương a , b sao cho điểm M có tọa độ ( a ; b2 + 3 ) và điểm N có tọa độ ( \(\sqrt{ab}\) ; 2 ) cùng thuộc đồ thị của hàm số y = x2
Những câu hỏi liên quan
9 tháng 1 2023 lúc 21:20
Cho hàm số: `y=x^2` và `y=-x+2`
`a,` Tìm tọa độ giao điểm của đồ thị `2` hàm số trên và tọa độ tung điểm `I` của đoạn thẳng `AB` biết điểm `A` có hoành độ dương
`b,` Tìm tọa độ điểm `M in (P): y =x^2` sao cho `ΔAMB` cân
\(S=\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{43.46}\\ =1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{43}-\dfrac{1}{46}\\ =1-\dfrac{1}{46}\\ =\dfrac{45}{46}\\ \Rightarrow S< 1\)
Đúng 0
Bình luận (0)
Gọi ` ƯCLN(n+1 ; 2n+3)=d`
Ta có:
`n+1 vdots d => 2n+2 vdots d`
`2n+3 vdots d`
`=>(2n+3)-(2n+2) vdots d`
`=>2n+3-2n-2 vdots d`
`=>1 vdots d`
`=>ƯCLN(n+1; 2n+3)=1`
`=> (n+1)/(2n+3)` tối giản
Đúng 0
Bình luận (0)
Gọi ` ƯCLN(2n+1,3n+4)=d`
Ta có:
`2n+1 vdots d => 6n+3 vdots d`
`3n +4 vdots d =>6n+8 vdots d`
`=>(6n+8)-(6n+3) vdots d`
`=>6n+8-6n-3 vdots d`
`=>5 vdots d`
Giả sử phân số rút gọn được
`=>2n+1 vdots 5`
`=>2n+1+5 vdots 5`
`=>2n+6 vdots 5`
`=>2(n+3) vdots 5`
`=>n+3 vdots 5`
`=>n = 5k-3`
`=> n ne 5k-3`
Vậy để phân số trên tối giản thì ` n ne 5k-3`
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
−
3
x
2
−
2.
Tìm số thực dương m để đường thẳng
y
m
cắt đồ thị hàm số tại 2 điểm phân biệt A, B sao cho tam giác OAB vuông tại O, trong đó O là gốc tọa độ. A.
m
2
B.
m
3
2
C.
m
3...
Đọc tiếp
Cho hàm số y = x 4 − 3 x 2 − 2. Tìm số thực dương m để đường thẳng y = m cắt đồ thị hàm số tại 2 điểm phân biệt A, B sao cho tam giác OAB vuông tại O, trong đó O là gốc tọa độ.
A. m = 2
B. m = 3 2
C. m = 3
D. m = 1
ĐAp án A
Phương trình hoành độ giao điểm là: x 4 − 3 x 2 − 2 − m = 0 1
Gọi A x ; m ; B − x ; m là tọa độ giao điểm
Khi đó Δ O A B vuông tại O khi O A ¯ . O B ¯ = − x 2 + m 2 = 0 ⇔ x = m
Khi đó m 4 − 3 m 2 − 2 − m = 0 ⇔ m = 2 (thỏa mãn).
Đúng 0
Bình luận (0)
cho hàm số y=x2 có đồ thị là parabol (P) và hàm số y=x+2 có đồ thị là đường thảng d
a) cmr: (P) luôn cắt (d) tại hai điểm phân biệt A,B. tìm tọa độ 2 điểm đó
b) xác định M có hoành độ dương trên (P) sao cho M cách đều 2 điểm A và B
Tìm tất cả các giá trị thực của m để đồ thị hàm số có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 với O là gốc tọa độ. A. . B. . C. . D. .
Đọc tiếp
Tìm tất cả các giá trị thực của m để đồ thị hàm số 
có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 với O là gốc tọa độ.
A. 
.
B. 
.
C. 
.
D. 
.
Chọn B.
Ta có: 
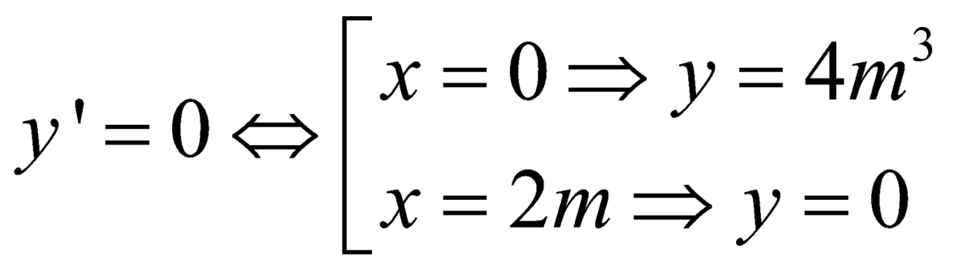
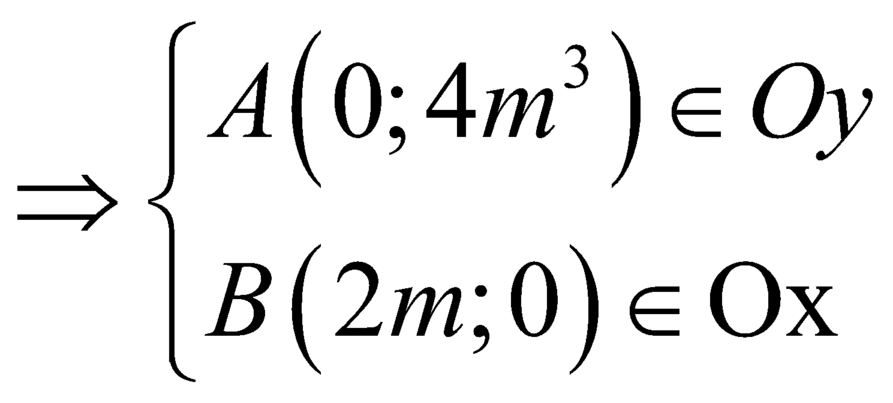
Do 3 điểm O,A, B không thẳng hàng nên
Ta có 
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho điểm A (-1;3) và đường thẳng ∆ có phương trình là x – 2y + 2 0. Dựng hình vuông ABCD sao cho hai đỉnh B, C nằm trên ∆. Tìm tọa độ điểm C biết C có tung độ dương. A. C (-2;0) B. C (0;1) C. C(2;2) D. C(1;4)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho điểm A (-1;3) và đường thẳng ∆ có phương trình là x – 2y + 2 = 0. Dựng hình vuông ABCD sao cho hai đỉnh B, C nằm trên ∆. Tìm tọa độ điểm C biết C có tung độ dương.
A. C (-2;0)
B. C (0;1)
C. C(2;2)
D. C(1;4)
Trong mặt phẳng tọa độ Oxy, cho điểm A (-1;3) và đường thẳng ∆ có phương trình là x – 2y + 2 0. Dựng hình vuông ABCD sao cho hai đỉnh B, C nằm trên ∆. Tìm tọa độ điểm C biết C có tung độ dương A. C (-2;0) B. C (0;1) C. C(2;2) D. C(1;4)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho điểm A (-1;3) và đường thẳng ∆ có phương trình là x – 2y + 2 = 0. Dựng hình vuông ABCD sao cho hai đỉnh B, C nằm trên ∆. Tìm tọa độ điểm C biết C có tung độ dương
A. C (-2;0)
B. C (0;1)
C. C(2;2)
D. C(1;4)
cho hàm số y=x2 có đồ thị là parabol (P) và hàm số y=x+2 có đồ thị là đường thảng d
a) cmr: (P) luôn cắt (d) tại hai điểm phân biệt A,B. tìm tọa độ 2 điểm đó
b) xác định M có hoành độ dương trên (P) sao cho M cách đều 2 điểm A và B
GIÚP MÌNH VỚI Ạ
a/ Phương trình hoành độ giao điểm y=x^2 và y=x+2
=>x^2=x+2
<=>x^2-x-2=0
denta=1-4*(-2)=9
x1=2=>y=4(2;4)
x2=-1=>y=1(-1;1)
M(0,5;2,5)
Đúng 0
Bình luận (0)
Cho hàm số bậc nhất y=ax+b có đồ thị đi qua điểm M(1;4). Biết rằng đồ thị của hàm số đã cho cát trục Ox tại điểm P có hoành độ dương và cắt trục Oy tại điểm Q có tung độ dương. Tìm a, b sao cho OP+OQ nhỏ nhất ( Với O là gốc tọa độ )
Gọi m là số thực dương sao cho đường thẳng
y
m
+
1
cắt đồ thị hàm số
y
x
4
−
3
x
2
−
2
tại hai điểm A, B thỏa mãn tam giác OAB vuông tại O (O là gốc tọa độ). Kết luận nào sau đây là đúng? A.
m
∈
7
9
;...
Đọc tiếp
Gọi m là số thực dương sao cho đường thẳng y = m + 1 cắt đồ thị hàm số y = x 4 − 3 x 2 − 2 tại hai điểm A, B thỏa mãn tam giác OAB vuông tại O (O là gốc tọa độ). Kết luận nào sau đây là đúng?
A. m ∈ 7 9 ; 9 4
B. m ∈ 1 2 ; 3 4
C. m ∈ 3 4 ; 5 4
D. m ∈ 5 4 ; 7 4
