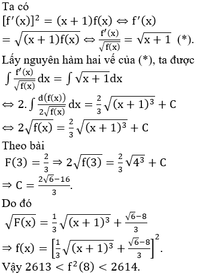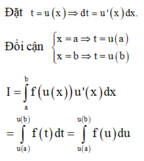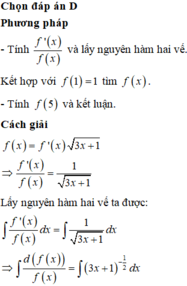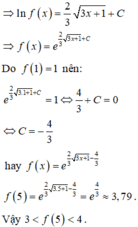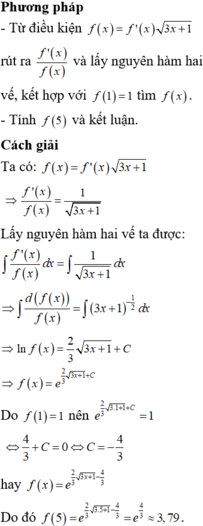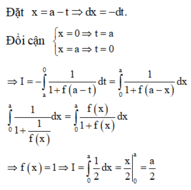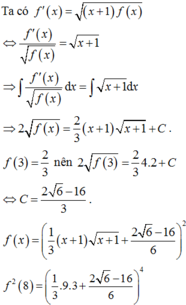Giả sử hai hàm số y = f(x) và y = f(x + 0,5) đều liên tục trên đoạn [0; 1] và f(0) = f(1). Chứng minh rằng phương trình f(x) − f(x + 0,5) = 0 luôn có nghiệm trong đoạn [0; 0,5]

Những câu hỏi liên quan
Cho hàm số y f(x) liên tục trên [a;b]. Giả sử hàm số u u(x) có đạo hàm liên tục trên [a;b] và
u
(
x
)
∈
[
α
;
β
]
∀
x
∈
[
a
;
b
]
hơn nữa f(u) liên...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a;b]. Giả sử hàm số u = u(x) có đạo hàm liên tục trên [a;b] và u ( x ) ∈ [ α ; β ] ∀ x ∈ [ a ; b ] hơn nữa f(u) liên tục trên đoạn [a;b]. Mệnh đề nào sau đây là đúng?
A. ∫ a b f ( u ( x ) ) u ' d x = ∫ u ( a ) u ( b ) f ( u ) d u
B. ∫ a b f ( u ( x ) ) u ' d x = ∫ a b f ( u ) d u
C. ∫ u ( a ) u ( b ) f ( u ( x ) ) u ' d x = ∫ a b f ( u ) d u
D. ∫ a b f ( u ( x ) ) u ' d x = ∫ a b f ( x ) d x
Phương pháp: Sử dụng phương pháp đổi biến, đặt t = u(x)
Cách giải:
Đặt
![]()
Đổi cận 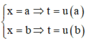
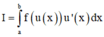

Đúng 0
Bình luận (0)
Cho hàm số y f(x) liên tục trên R và a 0. Giả sử rằng với mọi
x
∈
0
;
a
, ta có f(x) 0 và f(x)f(a – x) 1. Tính
I
∫
0
a
d
x
1
+
f
(
x
)
. A.
a...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và a > 0. Giả sử rằng với mọi x ∈ 0 ; a , ta có f(x) > 0 và f(x)f(a – x) = 1. Tính I = ∫ 0 a d x 1 + f ( x ) .
A. a 2 .
B. 2a.
C. a 3 .
D. aln(a + 1).
Chọn A.
Từ giả thiết, suy ra f a - x = 1 f x
Đặt t=a-x suy ra dt=-dx . Đổi cận: x = 0 → t = a x = a → t = 0
Khi đó
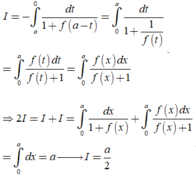
Đúng 0
Bình luận (0)
Giả sử hàm số y f(x) đồng biến trên
(
0
;
+
∞
)
; liên tục và nhận giá trị dương trên
(
0
;
+
∞
)
và thỏa mãn
f
(
3
)...
Đọc tiếp
Giả sử hàm số y = f(x) đồng biến trên ( 0 ; + ∞ ) ; liên tục và nhận giá trị dương trên ( 0 ; + ∞ ) và thỏa mãn f ( 3 ) = 2 3 và [ f ' ( x ) ] 2 = ( x + 1 ) . f ( x ) . Mệnh đề nào dưới đây đúng?
A . 2613 < f 2 ( 8 ) < 2614 .
B. 2614 < f 2 ( 8 ) < 2615 .
C. 2618 < f 2 ( 8 ) < 2619 .
D. 2616 < f 2 ( 8 ) < 2617 .
Cho hàm số y f(x) liên tục trên [a;b] Giả sử hàm số u u(x) có đạo hàm liên tục trên [a;b] và
u
(
x
)
∈
[
a
;
b
]
hơn nữa u(x) liên tục trên đoạn [a;b]Mệnh đề nào sau đây là đúng?
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a;b] Giả sử hàm số u = u(x) có đạo hàm liên tục trên [a;b] và u ( x ) ∈ [ a ; b ] hơn nữa u(x) liên tục trên đoạn [a;b]Mệnh đề nào sau đây là đúng?
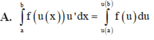
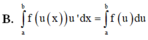
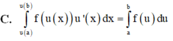

Giả sử hàm số yf(x) liên tục, nhận giá trị dương trên (0;+∞) và thỏa mãn f(1)1,
f
(
x
)
f
(
x
)
3
x
+
1
, với mọi x0. Mệnh đề nào sau đây đúng A. 1f(5)2 B. 4f(5)5 C. 2f(5)3 D. 3f(5)4
Đọc tiếp
Giả sử hàm số y=f(x) liên tục, nhận giá trị dương trên (0;+∞) và thỏa mãn f(1)=1, f ( x ) = f ' ( x ) 3 x + 1 , với mọi x>0. Mệnh đề nào sau đây đúng
A. 1<f(5)<2
B. 4<f(5)<5
C. 2<f(5)<3
D. 3<f(5)<4
Giả sử hàm số yf(x) liên tục, nhận giá trị dương trên
0
;
+
∞
và thỏa mãn f(1)1,
f
(
x
)
f
(
x
)
3
x
+
1
, với mọi x0. Mệnh đề nào sau đây đúng?
Đọc tiếp
Giả sử hàm số y=f(x) liên tục, nhận giá trị dương trên 0 ; + ∞ và thỏa mãn f(1)=1, f ( x ) = f ' ( x ) 3 x + 1 , với mọi x>0. Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
Cho số thực a0. Giả sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).(fa-x) 1 Tính tích phân
∫
0
1
1
1
+
f
(
x
)
d
x
A. I a/2 B. I a C. I 2a/3 D. I a/3
Đọc tiếp
Cho số thực a>0. Giả sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).(fa-x) = 1 Tính tích phân ∫ 0 1 1 1 + f ( x ) d x
A. I = a/2
B. I = a
C. I = 2a/3
D. I = a/3
Cho số thực a0. Giả sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a – x) 1,
∀
x
∈
[0;a]. Tính tích phân
I
∫
0
a
1
1
+
f
(
x
)...
Đọc tiếp
Cho số thực a>0. Giả sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a – x) = 1, ∀ x ∈ [0;a]. Tính tích phân I = ∫ 0 a 1 1 + f ( x ) d x
Đáp án A
Phương pháp : Sử dụng phương pháp đổi biến, đặt x = a – t.
Cách giải : Đặt x = a – t => dx = –dt. Đổi cận 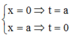
=> 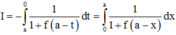
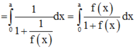
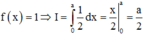
Đúng 0
Bình luận (0)
Giả sử hàm số yf(x) liên tục, nhận giá trị dương trên khoảng (0;+∞) và có f(3)2/3,
f
x
x
+
1
f
x
. Mệnh đề nào sau đây đúng? A.
2613
f
2
8
2614
B.
2618
f...
Đọc tiếp
Giả sử hàm số y=f(x) liên tục, nhận giá trị dương trên khoảng (0;+∞) và có f(3)=2/3, f ' x = x + 1 f x . Mệnh đề nào sau đây đúng?
A. 2613 < f 2 8 < 2614
B. 2618 < f 2 8 < 2619
C. 2614 < f 2 8 < 2615
D. 2616 < f 2 8 < 2617