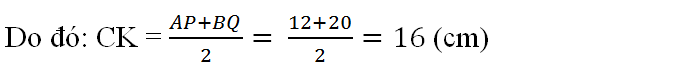Tính khoảng cách từ điểm A(2; 4; -3) lần lượt đến các mặt phẳng sau: x = 0 ( γ;)

Những câu hỏi liên quan
2 điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A --> xy bằng 12cm. Khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy
Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.
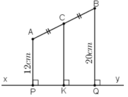
Gọi P, Q, K lần lượt là chân đường vuông góc hạ từ A, B, C xuống xy.
+ AP ⊥ xy và BQ ⊥ xy ⇒ AP // BQ
⇒ Tứ giác ABQP là hình thang.
+ CK ⊥ xy ⇒ CK // AP//BQ
+ Hình thang ABQP có AC = CB (gt) và CK // AP // BQ
⇒ PK = KQ
⇒ CK là đường trung bình của hình thang
⇒ CK = (AP + BQ)/2.
Mà AP = 12cm, BQ = 20cm ⇒ CK = 16cm.
Vậy khoảng cách từ trung điểm C của AB đến xy bằng 16cm.
Đúng 0
Bình luận (0)
: Kinh độ của 1 điểm là
A. khoảng cách tính bằng độ từ điểm đó đến xích đạo.
B. khoảng cách tính bằng độ từ điểm đó đến cực.
C. khoảng cách tính bằng độ từ điểm đó đến vĩ tuyến đi qua điểm đó.
khoảng cách tính bằng độ từ kinh tuyến gốc đến kinh tuyến đi qua điểm đó
Xem thêm câu trả lời
a) Hãy biểu diễn hai số -5 và 5 trên cùng một trục số.
b) Tính khoảng cách từ điểm 5 đến điểm 0.
c) Tính khoảng cách từ điểm -5 đến điểm 0.
a)

b) Khoảng cách từ điểm 5 đến điểm 0 là: 5 đơn vị
c) Khoảng cách từ điểm - 5 đến điểm 0 là: 5 đơn vị
Đúng 0
Bình luận (0)
tính khoảng cách điiểm gốc o đến mỗi điểm M,Q,R theo mẫu M -6 N -2 0 1 P Q R 7
mẫu khoảng cách từ 0 đến điểm N là 2 đơn vị
khoảng cách từ 0 đến P là 1 đơn vị
b) tính khoảng cách từ điểm gốc 0đến các điểm biểu diễn các số:-8;6;-50;15
Hai điểm A và B thuộc cùng một nữa mặt phẳng có bờ là đường thẳng xy, khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20 cm. Tính khoảng cách từ trung điểm C của AB đến xy
Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20 cm. Tính khoảng cách từ trung điểm C của AB đến xy ?
Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.
Kẻ AH, CM, BK vuông góc với xy (H, M, K là chân đường vuông góc).
Hình thang ABKH có AC = CB,
CM // AH // BK
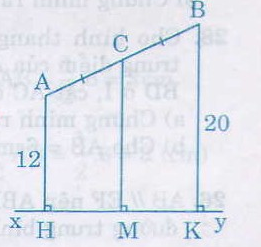
nên MH = MK và CM là đường trung bình.
Do đó CM = = 16 (cm)
Đúng 0
Bình luận (0)
Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.
Gọi P, Q, K lần lượt là chân đường vuông góc hạ từ A, B, C xuống xy.
+ AP ⊥ xy và BQ ⊥ xy => AP // BQ
=> Tứ giác ABQP là hình thang.
+ CK ⊥ xy => CK // AP// BQ
+ Hình thang ABQP có AC = CB ( gt ) và CK // AP // BQ
=> PK = KQ
=> CK là đường trung bình của hình thang
=> CK = (AP + BQ)/2
Mà AP = 12cm, BQ = 20cm => CK = 16cm.
Vậy khoảng cách từ trung điểm C của AB đến xy bằng 16cm .
Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A đến đường thẳng xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.