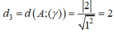Các câu hỏi tương tự
Tính khoảng cách từ điểm M(1; 2; 0) lần lượt đến các mặt phẳng sau: ( γ ): z + 5 = 0
Tính khoảng cách từ điểm A(2; 4; -3) lần lượt đến các mặt phẳng sau: 12x – 5z + 5 = 0 ( β)
Tính khoảng cách từ điểm A(2; 4; -3) lần lượt đến các mặt phẳng sau: 2x – y + 2z – 9 = 0 (α)
Tính khoảng cách từ điểm M(1; 2; 0) lần lượt đến các mặt phẳng sau: ( α ): x + 2y – 2z + 1 = 0
Tính khoảng cách từ điểm M(1; 2; 0) lần lượt đến các mặt phẳng sau: ( β ): 3x + 4z + 25 = 0
Cho hai đường thẳng chéo nhau:
d
:
x
2
-
t
y
-
1
+
t
z
1
-
t
d...
Đọc tiếp
Cho hai đường thẳng chéo nhau: d : x = 2 - t y = - 1 + t z = 1 - t d ' : x = 2 + 2 t y = t z = 1 + t
Lấy hai điểm M(2; -1; 1) và M'(2; 0; 1) lần lượt trên d và d'. Tính khoảng cách từ M đến mặt phẳng ( β) và khoảng cách từ M' đến mặt phẳng (α). So sánh hai khoảng cách đó.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y + 2z + 4 = 0 và điểm A(1;-2; 3). Tính khoảng cách từ điểm A đến mặt phẳng (P).
A. 7 3
B. 2
C. 14 2
D. 1
Trong không gian với hệ tọa độ Oxyz, cho điểm M(4;1;9). Gọi (P) là mặt phẳng đi qua M và cắt 3 tia Ox, Oy, Oz lần lượt tại các điểm A,B,C (khác 0) sao cho (OA+OB+OC) đạt giá trị nhỏ nhất. Tính khoảng cách d từ điểm I(0;1;3) đến mặt phẳng (P). A. d
34
5
B. d
36
5
C. d
24
7
D. d
30
7
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(4;1;9). Gọi (P) là mặt phẳng đi qua M và cắt 3 tia Ox, Oy, Oz lần lượt tại các điểm A,B,C (khác 0) sao cho (OA+OB+OC) đạt giá trị nhỏ nhất. Tính khoảng cách d từ điểm I(0;1;3) đến mặt phẳng (P).
A. d= 34 5
B. d= 36 5
C. d= 24 7
D. d= 30 7
Gọi H,I,K lần lượt là trung điểm các cạnh AB,CC’,A’C’. Tính khoảng cách từ điểm B’ đến mặt phẳng (HIK)? A.
d
(
B
,
(
H
I
K
)
)
5
2...
Đọc tiếp
Gọi H,I,K lần lượt là trung điểm các cạnh AB,CC’,A’C’. Tính khoảng cách từ điểm B’ đến mặt phẳng (HIK)?
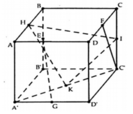
A. d ( B ' , ( H I K ) ) = 5 2 14 ( c m )
B. d ( B ' , ( H I K ) ) = 5 14 2 ( c m )
C. d ( B ' , ( H I K ) ) = 5 4 ( c m )
D. d ( B ' , ( H I K ) ) = 14 2 ( c m )