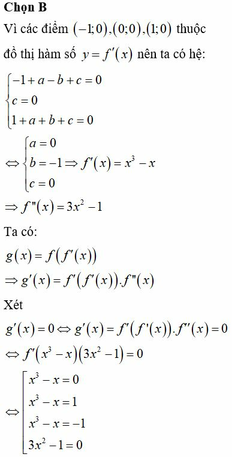cíuuu tớ vs tớ cần gấp ạaaaaaa:<

Những câu hỏi liên quan
cho hàm số y=f(x)=-x^2-2x+1. Mệnh đề nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng (-1;+vô cực) B. Hàm số nghịch biến trên khoảng (-vô cực;-1) C. Hàm số đồng biến trên khoảng (-1;+vô cực) D. Hàm số đồng biến trên khoảng (-vô cực;0)
B. Hàm số nghịch biến trên khoảng \(\left(-\infty;-1\right)\)
Đúng 3
Bình luận (0)
Cho hàm số y f(x), hàm số
f
x
x
3
+
a
x
2
+
b
x
+
c
a
,
b
,
c
∈
R có đồ thị như hình vẽHàm số
g
x
f
f...
Đọc tiếp
Cho hàm số y = f(x), hàm số f ' x = x 3 + a x 2 + b x + c a , b , c ∈ R có đồ thị như hình vẽ
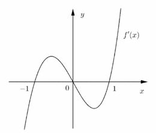
Hàm số g x = f f ' x nghịch biến trên khoảng nào dưới đây?
A. 1 ; + ∞
B. - ∞ ; - 2
C. - 1 ; 0
D. - 3 3 ; 3 3
Chỉ ra khoảng đồng biến, nghịch biến của hàm số: y = ax2 + bx + c, trong mỗi trường hợp a > 0 ; a < 0.
Xét sự biến thiên của hàm số f(x)=x+1x1x trên khoảng (1; dương vô cực). Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng (1; dương vô cực)
B. Hàm số nghịch biến trên khoảng (1; dương vô cực)
C. Hàm số đồng biến trên khoảng (-1;1)
D. Hàm số nghịch biến trên khoảng (âm vô cực; 1)
Mọi người giải ra giúp mình với ạ
Cho hs y= x^3-mx^2 +3(m-1)x+1 Tìm m để: a, Hs có cực đại cực tiểu |Xcd-Xct|=2 b, hs đạt cực đại tại x=2 c, hs đồng biến tren R d, hs đồng biến tren(1;dương vô cùng) e, hs nghịch biến trên đoạn có độ dài trên trục bằng 2
Xét tính đồng biến, nghịch biến của hàm số y=$\sqrt{x+3}$ trên (3; dương vô cực) Lm giúp MK với. Please!!
cho phương trình ax2 + bx + c = 0 vô nghiệm ( a>0)
CMR: ax2 + bx + c > 0 với mọi x thuộc R
Vì PTVN nên Δ<0
=>f(x)=ax^2+bx+c luôn cùng dấu với a
=>f(x)>0 với mọi x
Đúng 0
Bình luận (0)
xét tính đồng biến - nghịch biến của hàm số : y = \(\frac{2x+1}{x-1}\) trên ( 1 ; dương vô cực )
Lời giải:
$D=(1; +\infty)$
Ta có $y'=\frac{-3}{(x-1)^2}< 0$ với mọi $x\in (1;+\infty)$
Do đó hàm số luôn nghịch biến trên $(1;+\infty)$
Chứng tỏ rằng hàm số y= f(x) = x^2 - 4x +3 nghịch biến trong khoảng (- vô cực ; 2) và đồng biến trong khoảng (2: vô cực)