Cho tam giác ABC vuông tại A có 𝐴𝐵 = 3 ; 𝐴𝐶 = 1. Trên cạnh AB lấy các điểm M, N sao cho 𝐴𝑀 = 𝑀𝑁 = 𝑁𝐵.
a. Tính độ dài đoạn 𝐶𝑀.
b. Chứng minh rằng tam giác CMN đồng dạng tam giác BMC.
c. Chứng minh rằng ∠𝐶𝐵𝐴 + ∠𝐶𝑁𝐴 = 450
Những câu hỏi liên quan
Câu 1. Tính diện tích tam giác ABC trong các trường hợp sau:
a) ABC là tam giác đều có cạnh 𝐴𝐵 = 6cm.
b) ABC là tam giác vuông tại A, có 𝐴𝐵𝐶 ̂ = 30𝑜 , 𝐴𝐶 = 2𝑐𝑚.
c) ABC là tam giác cân tại A, có 𝐴𝐶 = 5𝑐𝑚, 𝐵𝐶 = 6cm.
Câu 1. Tính diện tích tam giác ABC trong các trường hợp sau:
a) ABC là tam giác đều có cạnh 𝐴𝐵 = 6cm.
b) ABC là tam giác vuông tại A, có 𝐴𝐵𝐶 ̂ = 30𝑜 , 𝐴𝐶 = 2𝑐𝑚.
c) ABC là tam giác cân tại A, có 𝐴𝐶 = 5𝑐𝑚, 𝐵𝐶 = 6cm.
a, Nửa chu vi là \(\frac{6+6+6}{2}=9cm\)
Diện tích tam giác là \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{9\left(9-6\right)\left(9-6\right)\left(9-6\right)}\)
\(=\sqrt{9.3.3.3}=9\sqrt{3}\)cm2
b, Xét tam giác ABC vuông tại A
tan^B = \(\frac{AC}{AB}\Rightarrow\frac{\sqrt{3}}{3}=\frac{2}{AB}\Rightarrow AB=\frac{6\sqrt{3}}{3}=2\sqrt{3}\)cm
Diện tích tam giác là \(\frac{1}{2}AB.AC=6\sqrt{3}\)cm2
c, Dựng AH là đường cao đồng thời là đường trung tuyến do tam giác ABC cân tại A
=> HC = BC/2 = 3 cm
Theo định lí Pytago tam giác AHC vuông tại H
\(AH=\sqrt{AC^2-HC^2}=4cm\)
Diện tích tam giác ABC là : \(\frac{1}{2}AH.BC=\frac{4.6}{2}=12cm^2\)
Bài 2: Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của AB và BC. a) Giả sử 𝐴𝐵 = 6𝑐𝑚, 𝐵𝐶 = 10𝑐𝑚, tính diện tích tam giác AMC.
\(AM=MC=5cm\)
AC=8cm
\(S=\dfrac{4\cdot3}{2}=6\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác 𝐴𝐵𝐶 vuông tại 𝐴 với 𝐴𝐵 = 3 𝑐𝑚; 𝐴𝐶 = 4 𝑐𝑚; vẽ đường cao 𝐴𝐸. a Chứng minh ∆𝐴𝐵𝐶 đồng dạng với ∆𝐸𝐵𝐴. b Chứng minh 𝐴𝐵² = 𝐵𝐸. 𝐵𝐶. c Tia phân giác của góc 𝐴𝐵𝐶 cắt 𝐴𝐶 tại 𝐹. Tính độ dài 𝐴𝐹.
a: Xet ΔABC và ΔEBA có
góc BAC=góc BEA
góc B chung
=>ΔABC đồng dạng với ΔEBA
b: ΔABC vuông tại A có AE vuông góc BC
nên AB^2=BE*BC
c: BF là phân giác
=>AF/AB=CF/BC
=>AF/3=FC/5=4/8=1/2
=>AF=1,5cm
Đúng 2
Bình luận (0)
Cho tam giác ABC cân ở A, có 𝐴𝐵 = 10𝑐𝑚,𝐵𝐶 = 12𝑐𝑚. Tính độ dài phân giác AD của tam giác ABC.
Cho tam giác 𝐴𝐵𝐶 vuông tại 𝐴, có 𝐴𝐵 9 𝑐𝑚; 𝐴𝐶 12 𝑐𝑚. Tia phân giác góc 𝐴 cắt 𝐵𝐶 tại 𝐷, từ 𝐷 kẻ 𝐷𝐸 vuông góc với 𝐴𝐶 (𝐸 ∈ 𝐴𝐶). a Tính tỉ số𝐵𝐷/CD Chứng minh: ∆𝐴𝐵𝐶 ∽ ∆𝐸𝐷𝐶.
Đọc tiếp
Cho tam giác 𝐴𝐵𝐶 vuông tại 𝐴, có 𝐴𝐵 = 9 𝑐𝑚; 𝐴𝐶 = 12 𝑐𝑚. Tia phân giác góc 𝐴 cắt 𝐵𝐶 tại 𝐷, từ 𝐷 kẻ 𝐷𝐸 vuông góc với 𝐴𝐶 (𝐸 ∈ 𝐴𝐶). a Tính tỉ số𝐵𝐷/CD Chứng minh: ∆𝐴𝐵𝐶 ∽ ∆𝐸𝐷𝐶.
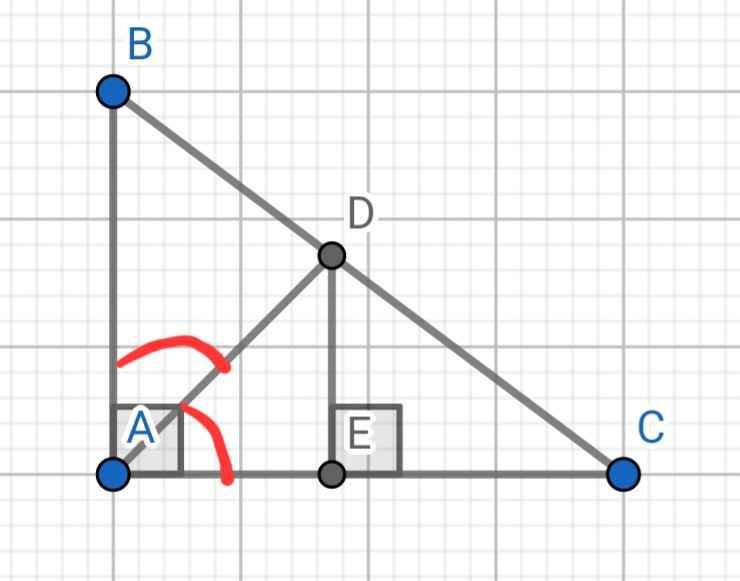
a) Do AD là đường phân giác của ∠BAC
⇒ BD/CD = AB/AC = 9/12 = 3/4
b) Xét hai tam giác vuông: ∆ABC và ∆EDC có:
∠C chung
⇒ ∆ABC ∽ ∆EDC (g-g)
Đúng 1
Bình luận (0)
a: BD/CD=AB/AC=3/4
b: Xét ΔABC vuông tại A và ΔEDC vuông tại E có
góc C chung
=>ΔABC đồng dạng với ΔEDC
Đúng 1
Bình luận (0)
1) Cho tam giác ABC vuông tại A có góc B = 60độ, AC = 3cm. Tính BC, AB
2) Cho tam giác ABC vuông tại A có BC = 10cm, góc C = 3cm. Tính góc B, AB, AC
3) Cho tam giác ABC vuông tại A có AB = 4cm, góc B = 50 độ. Tính BC, góc C, AC
3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
Đúng 0
Bình luận (1)
cho tam giác ABC có 3 góc nhọn. Vẽ về phía ngoài của tam giác ABC các tam giác ABK vuông tại A và tam giác CAD vuông tại A có AB=MB. Chứng minh:
a/ tam giác ACK= tam gic1 ABD
b/ KC vuông góc BD
cho tam giác ABC có 3 góc nhọn. Vẽ về phía ngoài của tam giác ABC các tam giác ABK vuông tại A và tam giác CAD vuông tại A có AB=MB. Chứng minh:
a/ tam giác ACK= tam gic1 ABD
b/ KC vuông góc BD
Cho tam giác ABC có 3 góc nhọn. Vẽ về phía ngoài của tam giác ABC và tam giác ABK vuông tại A và tam giác CAD vuông tại A có AB=AK; AC=AD. Chúng minh:
a, Tam giác ACK = Tam giác ABD
b, KC vuông góc với BD.