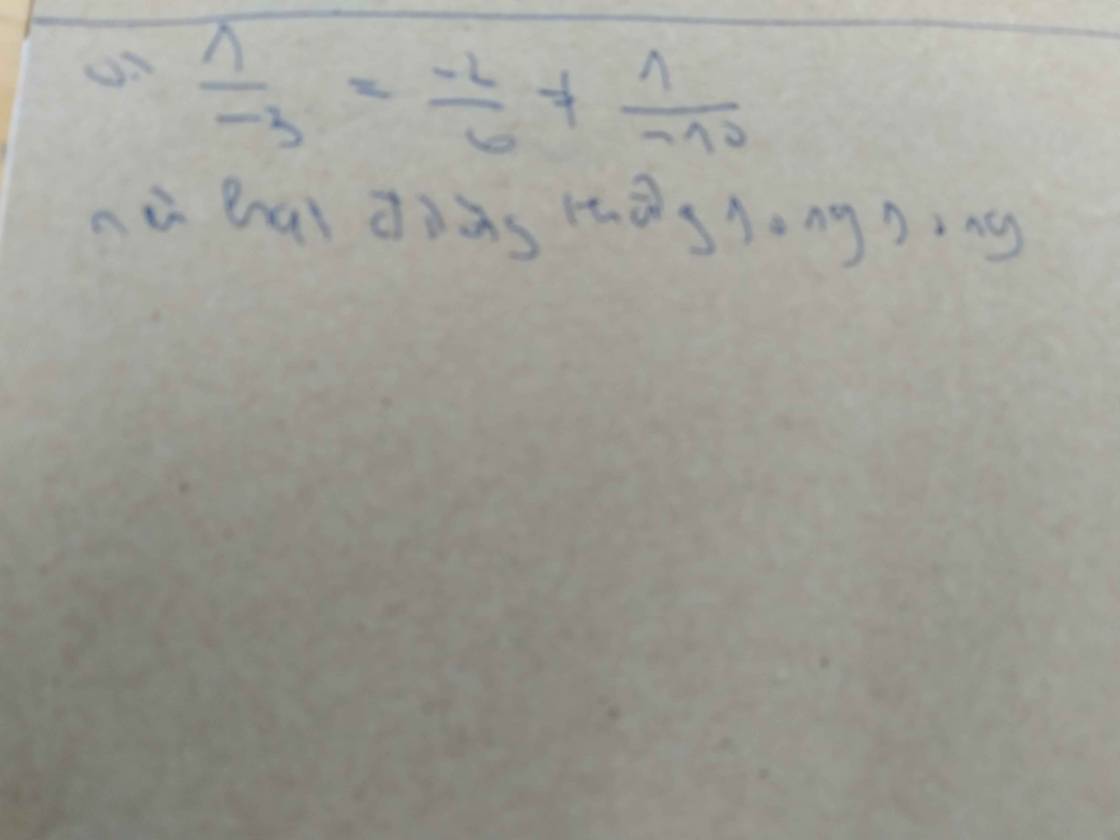xác định vị trí tương đối của 2 đường thẳng sau đây △1: x-2y+1=0; △2: -3x+6y-10=0
Những câu hỏi liên quan
Xác định vị trí tương đối của 2 đường thẳng sau đây: (d1): x- 2y+ 10 và (d2): -3x+ 6y-1 0 . A. Song song. B. Trùng nhau. C. Vuông góc nhau. D. Cắt nhau.
Đọc tiếp
Xác định vị trí tương đối của 2 đường thẳng sau đây: (d1): x- 2y+ 1=0 và (d2): -3x+ 6y-1 =0 .
A. Song song.
B. Trùng nhau.
C. Vuông góc nhau.
D. Cắt nhau.
Đường thẳng (d1) có vtpt 
và
d2 có vtpt 
Hai đường thẳng này có
nên hai đường thẳng này song song với nhau.
Chọn A.
Đúng 0
Bình luận (0)
xác định vị trí tương đối giữa 2 đường thẳng delta 1: x-2x+1=0 và delta 2: -3x-4y-1=0
Xem lại đề phương trình đường thẳng delta1
Đúng 0
Bình luận (0)
xác định vị trí tương đối giữa hai đường thảng delta1: x-2y+1=0 và delta2: -3x+6y-10=0
Do \(\dfrac{1}{-3}=\dfrac{-2}{6}\ne\dfrac{1}{-10}\) nên 2 đường thẳng đã cho song song
Đúng 1
Bình luận (1)
27 tháng 3 2016 lúc 12:00
xét vị trí tương đối của đường thẳng (d) và đường tròn (C) sau đây : (d) : 3x + y + m = 0 ; (C) : x2 + y2 - 4x + 2y + 1 = 0
Xét vị trí tương đối của đường thẳng Δ: x – 2y + 1 = 0 với mỗi đường thẳng sau:
d1: -3x + 6y – 3 = 0;
d2: y = -2x;
d3: 2x + 5 = 4y.
Xét Δ và d1, hệ phương trình: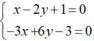 
có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
Xét Δ và d2, hệ phương trình: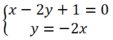 
có nghiệm duy nhất (-1/5; 2/5) nên
Δ cắt d2 tại điểm M(-1/5; 2/5).
Xét Δ và d3, hệ phương trình: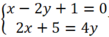 
vô nghiệm
Vậy Δ // d3
Đúng 0
Bình luận (0)
24 tháng 3 2016 lúc 11:47
xét vị trí tương đối của đường thẳng (d) và đường tròn (C) sau đây : (d) : 3x + y + m = 0 ; (C) : x2 + y2 - 4x + 2y + 1 =0
21 tháng 3 2016 lúc 19:11
xét vị trí tương đối của đường thẳng (d) và đường tròn (C) sau đây : (d) : 3x + y + m = 0 ; (C) : x2 + y2 - 4x + 2y + 1 =0
24 tháng 3 2016 lúc 19:07
xét vị trí tương đối của đường thẳng (d) và đường tròn (C) sau đây : (d) : 3x + y + m = 0 ; (C) : x2 + y2 - 4x + 2y + 1 =0
24 tháng 3 2016 lúc 21:18
xét vị trí tương đối của đường thẳng (d) và đường tròn (C) sau đây : (d) : 3x + y + m = 0 ; (C) : x2 + y2 - 4x + 2y + 1 =0