cho hình vẽ:
biết Aa// Cc
∠A125 độ; ∠C1 50 độ
Tính∠ABC
Đọc tiếp
cho hình vẽ:
biết Aa// Cc
∠A1=25 độ; ∠C1 = 50 độ
Tính∠ABC
Những câu hỏi liên quan
Cho hình lăng trụ tam giác ABC.A’B’C’ có thể tích là V và độ dài cạnh bên là AA’6 đơn vị. Cho điểm A1 thuộc cạnh AA’ sao cho AA12. Các điểm B1, C1 lần lượt thuộc cạnh BB’, CC’ sao cho BB1x, CC1y. Biết rằng thể tích khối đa diện ABC. A1B1C1 bằng 1/2V. Giá trị của x+y bằng A. 10 B. 4 C. 16 D. 7
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A’B’C’ có thể tích là V và độ dài cạnh bên là AA’=6 đơn vị. Cho điểm A1 thuộc cạnh AA’ sao cho AA1=2. Các điểm B1, C1 lần lượt thuộc cạnh BB’, CC’ sao cho BB1=x, CC1=y. Biết rằng thể tích khối đa diện ABC. A1B1C1 bằng 1/2V. Giá trị của x+y bằng
A. 10
B. 4
C. 16
D. 7
cho tam giac ABC .cac duong cao AA' BB',CC',cat nhau tai H. cac diem A1 B1 C1 doi xung qua BC, AC, BA. chung minh AA1/AA' +BB1/BB' + CC1/CC'
Cho tam giác ABC, trọng tâm G.
a/ Vẽ đường thẳng d đi qua G, cắt các đoạn thẳng AB, AC. Gọi A', B', C' là hình chiếu của A, B, C trên d. Tìm liên hệ giữa các độ dài AA', BB', CC'.
b/ Nếu đường thẳng d nằm ngoàn tam giác ABC và G' là hình chiếu của G trên d thì các độ dài AA', BB', CC' có liên hệ gì?
Cho tam giác ABC, trọng tâm G
a) Vẽ đường thẳng d qua G, cắt các đoạn thẳng AB, AC.Gọi A',B',C' là hình chiếu của A,B,C trên d. Tìm liên hệ giữa các độ dài AA', BB',CC'
b) Nếu đường thẳng d nằm ngoài tam giác ABC và G' là hình chiếu của G tren d thì các độ dài AA', BB',CC',GG' có liên hệ gì?
Trong nửa mặt phẳng trên đường thẳng xx',cho ba điểm A,B,C.Trong 1 mặt phẳng có bờ xx' người ta vẽ các tia Aa và Bb sao cho xAa=30 độ ,xBb=180 độ .Trong nửa mp kia vẽ tia Cc sao cho đg thẳng chứa tia Aa:
a)cmr:Hai đg thẳng Aa và Bb song song vs nhau
b)tìm số đo góc xCc.Nhờ các bạn giúp mìn vs nhé ,không vẽ hình cx đc ạ cảm ơn các bạn❤️
Cho tam giác ABC có 3 góc nhọn. 3 đường cao AA', BB', CC' cắt nhau tại H; A1, B1, C1 là các điểm đối xứng của H qua BC, AC,AB. CM: \(\dfrac{AA_1}{AA'}+\dfrac{BB_1}{BB'}+\dfrac{CC_1}{CC'}\) không đổi
trên đường thẳng xx' cho 3 điểm abc a thuộc ax c thuộc bx Trên nửa mặt phẳng Bxx' vẽ tia Aa Bb sao cho góc xAa=150 độ và xBb=30 độ trên nửa mặt phẳng còn lại vẽ tia Ccsao cho góc x'Cc=30 độ. Chứng minh Rằng 3 đường thẳng chứa ba tia Aa Bb Cc song song với nhau
Cho tam giác ABC có góc A bằng 120 độ. AA',BB',CC' theo thứ tự là tia phân giác của các góc A,góc B và góc C CMR: A'B' vuông góc với A'C' ----------------------giúp giải bài này nha !^_^------------------------------------------------------------------ # Lưu ý : vẽ hình nha các bạn vẽ hình mới được tick nha ^_^
Cho hình bình hành ABCD và đường thẳng xy không có điểm chung với hình bình hành. Gọi AA’; BB’; CC’, DD’ là các đường vuông góc kẻ từ A, B, C, D đến đường thẳng xy. Tìm mối liên hệ độ dài giữa AA', BB', CC', DD'
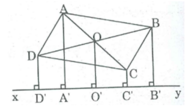
Gọi O là giao điểm của AC và BD
⇒ OA = OC, OB = OD (tính chất hình bình hành)
Kẻ OO' ⊥ xy
AA' ⊥ xy (gt)
CC' ⊥ xy (gt)
Suy ra: AA' // OO' // CC'
Tứ giác ACC'A' là hình thang có:
OA = OC (chứng minh trên)
OO' // AA' nên OO' là đường trung bình của hình thang ACC'A'.
⇒ OO' = (AA' + CC') / 2 (t/chất đường trung bình của hình thang) (1)
BB' ⊥ xy
DD' ⊥ xy (gt)
OO' ⊥ xy (gt)
Suy ra: BB'// OO' // DD'
Tứ giác BDD'B' là hình thang có:
OB = OD (Chứng minh trên)
OO' // BB' nên OO' là đường trung bình của hình thang BDD'B'.
⇒ OO' = (BB' + DD') / 2 (tính chất đường trung bình của hình thang) (2)
Từ (1) và (2) => AA' + CC' = BB + DD'
Đúng 0
Bình luận (0)
1. Cho tam giác ABC nội tiếp (O;R) và AA, BB, CC là 3 đường trung tuyến. Kéo dài 3 trung tuyến cắt (O;R) tại A1, B1, C1.Chứng minh: dfrac{AA}{AA_1}+dfrac{BB}{BB_1}+dfrac{CC}{CC_1}ledfrac{9}{4}2. Cho tam giác ABC nội tiếp (O;R) và AA, BB, CC là 3 đường cao. Kéo dài 3 đường cao cắt (O;R) tại A1, B1, C1.Chứng minh: dfrac{AA}{AA_1}+dfrac{BB}{BB_1}+dfrac{CC}{CC_1}gedfrac{9}{4}3. Cho tam giác ABC với O1, O2, O3 là tâm các đường trong bàng tiếp góc A, B, C. Gọi S1, S2, S3 lần lượt là diện tích các tam...
Đọc tiếp
1. Cho tam giác ABC nội tiếp (O;R) và AA', BB', CC' là 3 đường trung tuyến. Kéo dài 3 trung tuyến cắt (O;R) tại A1, B1, C1.
Chứng minh: \(\dfrac{AA'}{AA_1}+\dfrac{BB'}{BB_1}+\dfrac{CC'}{CC_1}\le\dfrac{9}{4}\)
2. Cho tam giác ABC nội tiếp (O;R) và AA', BB', CC' là 3 đường cao. Kéo dài 3 đường cao cắt (O;R) tại A1, B1, C1.
Chứng minh: \(\dfrac{AA'}{AA_1}+\dfrac{BB'}{BB_1}+\dfrac{CC'}{CC_1}\ge\dfrac{9}{4}\)
3. Cho tam giác ABC với O1, O2, O3 là tâm các đường trong bàng tiếp góc A, B, C. Gọi S1, S2, S3 lần lượt là diện tích các tam giác O1BC, O2CA, O3AB.
Chứng minh: \(S_1+S_2+S_3\ge3S\)