Cho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A và D, có A D = C D = a ; A B = 2 a ; S A ⊥ A B C D , E là trung điểm của AB. Khẳng định nào sau đây đúng?
A. C E ⊥ S D C
B. C B ⊥ S A B
C. Δ S C v u ô n g ở C
D. C E ⊥ S A B
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D với AD = 2a, AB = 2DC = 2a, SA ⊥ (ABCD) và cạnh SB tạo với đáy một góc 600. Thể tích khối chóp S.ABCD bằng
A. 2 a 3 3 3
B. a 3 3
C. 2 a 3 3
D. a 3
Phương pháp
+ Xác định góc giữa đường thẳng d và mặt phẳng (P) là góc giữa đường thẳng d và đường thẳng d' với d' là hình chiếu của d trên mặt phẳng (P).
+ Thể tích hình chóp có chiều cao h và diện tích đáy S là V = 1 3 h S
Cách giải:
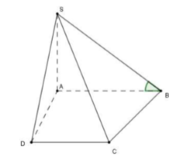
+ Ta có SA ⊥ (ABCD) => AB là hình chiếu của
SB lên mặt phẳng (ABCD) . Suy ra góc giữa SB và đáy là góc ∠ SBA = 600.
+ Xét tam giác vuông SAB có: ![]()
+ Diện tích đáy
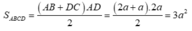
+ Thể tích khối chóp là
![]()
Chọn C.
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D với AD = 2a, AB = 2DC = 2a, S A ⊥ A B C D và cạnh SB tạo với đáy một góc 60 ° . Thể tích khối chóp S.ABCD bằng
A. 2 a 3 3 3
B. a 3 3
C. 2 a 3 3
D. a 3
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D; SD vuông góc với mặt đáy (ABCD). Tính khoảng cách giữa đường thẳng CD và mặt phẳng (SAB).

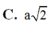
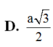
Cho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A và D, có ![]() là trung điểm của AB. Khẳng định nào sau đây đúng?
là trung điểm của AB. Khẳng định nào sau đây đúng?
![]()
![]()
![]()
![]()
cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, với AB=2a, AD=DC=a, SA vuông góc với đáy (ABCD) và SA=a.
Tính góc giữa (sdc) và (sbc)
THAM KHẢO
Mặt phẳng (SDC):
\(\overset{⃗}{S D} = D - S = \left(\right. 0 , a , - a \left.\right)\)\(\overset{⃗}{S C} = C - S = \left(\right. a , a , - a \left.\right)\)Pháp tuyến:

Mặt phẳng (SBC):
\(\overset{⃗}{S B} = B - S = \left(\right. 2 a , 0 , - a \left.\right)\)\(\overset{⃗}{S C} = \left(\right. a , a , - a \left.\right)\)Pháp tuyến:

3. Góc giữa hai mặt phẳng
\(cos \theta = \frac{\mid \overset{⃗}{n_{1}} \cdot \overset{⃗}{n_{2}} \mid}{\mid \overset{⃗}{n_{1}} \mid \cdot \mid \overset{⃗}{n_{2}} \mid}\)
\(\overset{⃗}{n_{1}} \cdot \overset{⃗}{n_{2}} = \left(\right. 0 \left.\right) \left(\right. - a^{2} \left.\right) + \left(\right. - a^{2} \left.\right) \left(\right. a^{2} \left.\right) + \left(\right. - a^{2} \left.\right) \left(\right. 2 a^{2} \left.\right) = - 3 a^{4} \Rightarrow \mid \cdot \mid = 3 a^{4}\)\(\mid \overset{⃗}{n_{1}} \mid = a^{2} \sqrt{0^{2} + 1^{2} + 1^{2}} = a^{2} \sqrt{2}\)\(\mid \overset{⃗}{n_{2}} \mid = a^{2} \sqrt{\left(\right. - 1 \left.\right)^{2} + 1^{2} + 2^{2}} = a^{2} \sqrt{6}\)\(\Rightarrow \&\text{nbsp}; cos \theta = \frac{3 a^{4}}{a^{4} \sqrt{12}} = \frac{3}{2 \sqrt{3}} = \frac{\sqrt{3}}{2}\)
Kết luận:
\(cos \theta = \frac{\sqrt{3}}{2} \Rightarrow \theta = 30^{\circ} .\)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, SA vuông góc với mặt phẳng đáy và SA = a; AD=CD=A; AB=2A.Gọi (α) là mặt phẳng qua A và vuông góc SB. Tính diện tích thiết diện của hình chóp khi cắt bởi mp (α)
Gặp những bài cần tính toán thế này làm biếng lắm, dựng hình thì dễ chứ tính thì chả muốn tính chút xíu nào.
Trong mp đáy, kéo dài AD và BC cắt nhau tại E \(\Rightarrow D\) là trung điểm AE (đường trung bình) \(\Rightarrow AE=AB=2a\)
Ta có: \(\left\{{}\begin{matrix}AD\perp AB\\SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\Rightarrow AD\perp SB\)
\(\Rightarrow AD\in\left(\alpha\right)\)
Trong mp (SAB), kẻ \(AM\perp SB\Rightarrow M\in\left(\alpha\right)\)
Dễ dàng chứng minh tam giác ACB vuông cân tại C (Pitago đảo) \(\Rightarrow BC\perp\left(SAC\right)\)
Trong mp (SAC), kẻ \(AN\perp SC\Rightarrow AN\perp\left(SBC\right)\Rightarrow AN\perp SB\Rightarrow N\in\left(\alpha\right)\)
\(\Rightarrow\) Thiết diện là tứ giác AMND
\(SB=SE=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(AM=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{2a\sqrt{5}}{5}\)
\(AC=a\sqrt{2}\Rightarrow SC=\sqrt{AC^2+SA^2}=a\sqrt{3}\)
\(CN=\dfrac{AC^2}{SC}=\dfrac{2a\sqrt{3}}{3}\) ; \(EC=BC=a\sqrt{2}\Rightarrow EN=\sqrt{EC^2+CN^2}=\dfrac{a\sqrt{30}}{3}\)
\(DE=AD=a\)
\(S_{AME}=\dfrac{1}{2}AM.AE=...\)
\(S_{DNE}=\dfrac{1}{2}DE.EN.sin\widehat{DEN}=\dfrac{1}{2}DE.EN.\dfrac{AM}{\sqrt{AM^2+AE^2}}=...\)
\(\Rightarrow S_{AMND}=S_{AME}-S_{DNE}=...\)
Trong trường hợp vuông góc SC:
Vẫn nối AD cắt BC tại E rồi chứng minh \(BC\perp\left(SAC\right)\)
Sau đó từ A kẻ \(AN\perp SC\)
Trong mp (SBE), qua N kẻ đường thẳng song song BE lần lượt cắt SB tại M và cắt SE tại I
Trong mp (SAD), nối AI cắt SD tại P
Tứ giác AMNP là thiết diện cần tìm
Như câu trước, tính được \(CN=\dfrac{2a\sqrt{3}}{3}\) ; \(SC=a\sqrt{3}\Rightarrow SN=\dfrac{a\sqrt{3}}{3}\)
Talet: \(\dfrac{SM}{SB}=\dfrac{SI}{SE}=\dfrac{SN}{SC}=\dfrac{IM}{EB}=\dfrac{1}{3}\Rightarrow SM=SI=\dfrac{1}{3}SB=\dfrac{a\sqrt{5}}{3};IM=\dfrac{EB}{3}=\dfrac{2a\sqrt{2}}{3}\)
\(AN=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=\dfrac{a\sqrt{6}}{3}\) \(\Rightarrow AI=AM=\sqrt{AN^2+\left(\dfrac{IM}{2}\right)^2}=\dfrac{2a\sqrt{2}}{3}\)
\(\Rightarrow\Delta AIM\) đều
Trong tam giác SAE, đặt \(\overrightarrow{AP}=x\overrightarrow{AI}\)
\(\overrightarrow{SP}=\overrightarrow{SA}+\overrightarrow{AP}=\overrightarrow{SA}+x.\overrightarrow{AI}=\overrightarrow{SA}+x\left(\overrightarrow{AS}+\overrightarrow{SI}\right)=\left(1-x\right)\overrightarrow{SA}+\dfrac{x}{3}\overrightarrow{SE}\)
D là trung điểm AE \(\Rightarrow\overrightarrow{SD}=\dfrac{1}{2}\overrightarrow{SA}+\dfrac{1}{2}\overrightarrow{SE}\)
Mà S; P; D thẳng hàng \(\Rightarrow\dfrac{1-x}{\dfrac{1}{2}}=\dfrac{\dfrac{x}{3}}{\dfrac{1}{2}}\Leftrightarrow1-x=\dfrac{x}{3}\Rightarrow x=\dfrac{3}{4}\)
\(\Rightarrow IP=\dfrac{1}{4}AI=\dfrac{a\sqrt{2}}{6}\)
\(S_{AMNP}=S_{AIM}-S_{IPN}=\dfrac{1}{2}AN.IM-\dfrac{1}{2}IP.IN.sin\widehat{PIN}\)
Với chú ý rằng \(IN=\dfrac{1}{2}IM=...\) và \(\widehat{PIN}=60^0\) do tam giác AIM đều theo cmt
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D, AD=AB=2a, CD=a góc giữa (SBC) với đáy bằng 60 ° , I là trung điểm của AD, (SBI), (SCI) vuông góc với đáy. Thể tích S.ABCD bằng
A. a 3 13 3
B. 3 a 3 15 5
C. 2 a 3 3 5
D. a 3 5 3
Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D. AB=2AD, AD=DC, BC=a√2. ∆SBC cân tại S và nằm trong mặt phẳng vuông góc với đág. SA hợp với đáy 1 góc 45°. Tính d(SA;BC)
Cho hình chóp S.ABCD có đáy ABCD là hính thang vuông tại A và B AB=BC=a , SA =a và vuông góc với mặt phẳng (ABCD) .Khoảng cách từ D đến mặt phẳng (SAC) bằng a√2. Tính thể tích V S.ABCD