Cho hình chóp S.ABCD có S A = a ; A B = B C = 2 a ; B A C ⏜ = 120 ° và cạnh bên SA vuông góc với mặt phẳng đáy. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp đã cho.
A. a 17 4
B. a 17 3
C. a 17 2
D. a 17 5
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD= 3 a 2 , hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD
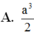
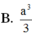
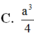
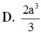
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên S A = 3 a 2 . Tính thể tích khối chóp S.ABCD theo a.
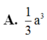
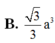
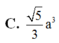
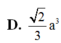
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên S D = 3 a 2 . Tính thể tích khối chóp S . A B C D theo a.
A. 1 3 a 3
B. 3 3 a 3
C. 5 3 a 3
D. 2 3 a 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên SD = 3 a 2 . Tính thể tích khối chóp S.ABCD theo a.
A. 1 3 a 3
B. 3 3 a 3
C. 6 3 a 3
D. 2 3 a 3
Đáp án A
Ta có A D = H A 2 + A D 2 = a 2 2 + a 2 = a 5 2 ⇒ S H = S D 2 - A D 2 = a
Thể tích khối chóp đã cho là: V = 1 3 S H . S A B C D = 1 3 a . a 2 = 1 3 a 3 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD = 13 2 . Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB. Thể tích khối chóp S.ABCD là:
A. a 3 2 3
B. a 3 12
C. a 3 3
D. 2 a 3 3
Đáp án A
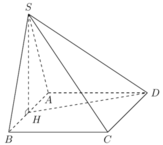
Ta có tam giác AHD vuông tại A, suy ra
H D = A H 2 + D H 2 = a 2 4 + a 2 = a 5 2
Tam giác SHD vuông tại H, suy ra:
S
H
=
S
D
2
-
H
D
2
=
13
a
2
4
-
5
a
2
4
=
a
2
Vậy V S . A B C D = a 3 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD
A. a 3 2
B. a 3 3
C. a 3 4
D. 2 a 3 3
Cho hình chóp S.ABCD có đáy ABCD hình vuông cạnh a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AD. Tính thể tích khối chóp S.ABCD biết SB = 3a/2.
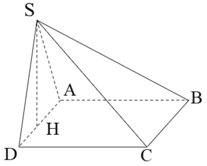
A. a 3 3
B. a 3
C. a 3 2
D. 3 a 3 2
Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm O và AB = a, BC = a \(\sqrt{3}\)
(SAD) ⊥ (ABCD), SD tạo với đáy một góc 60◦ và ∆SAO cân tại S. Tính thể tích khối chóp S.ABCD.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, S A = 2 a 2 , tam giác SAC vuông tại S và nằm trong mặt phẳng vuông góc với (ABCD). Tính theo a thể tích V của khối chóp S.ABCD.
A. V = 6 a 3 12
B. V = 6 a 3 3
C. V = 6 a 3 4
D. V = 6 a 3 6
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, S A = 2 a 2 , tam giác SAC vuông tại S và nằm trong mặt phẳng vuông góc với (ABCD). Tính theo a thể tích V của khối chóp S.ABCD
A. V = 6 a 3 12
B. V = 6 a 3 3
C. V = 6 a 3 4
D. V = 2 a 3 6

Vẽ S H ⊥ A C tại H.
Khi đó: ( S A C ) ⊥ ( A B C D ) ( S A C ) ⊥ ( A B C D ) = A C S H ⊂ ( S A C ) S H ⊥ A C
⇒ S H ⊥ ( A B C D ) ⇒ V = 1 3 S H . S A B C D
Theo đề ∆ S A C vuông tại S nên ta có:
S C = A C 2 - S A 2 = 6 a 2
và S H = S A . S C A C
= 2 a 2 . 6 a 2 2 a = 6 a 4
Vậy V = 1 3 S H . S A B C D = 6 a 3 12
Chọn đáp án A.