Cho ΔABC có \(\widehat{ABC}=50^0\); \(\widehat{BAC}=70^0\). Phân giác trong góc ACB cắt AB tại M. Trên MC lấy điểm N sao cho \(\widehat{MBN}=40^0\). Chứng mỉnh rằng BN = MC

Những câu hỏi liên quan
cho tam giác ABC vuông tại C có \(\widehat{A}< \widehat{B}\). gọi I, O thứ tự là tâm đường tròn nội tiếp, ngoại tiếp ΔABC. biết ΔBIO vuông . tính tỉ số các cạnh của ΔABC
Cho ΔABC cân tại A có \(\widehat{A}\)= \(^{50^0}\); M là trung điểm của BC khi đó:
a) Tính góc B
b) Chứng minh AM ⊥BC
c) Chứng minh AM là phân giác \(\widehat{BAC}\)
a, tam giác ABC cân tại A (gt)
=> góc B = (180 - góc A) : 2
góc A = 50 (gt)
=> góc B = (180 - 50) : 2
=> góc B = 65
b, xét tam giác AMB và tam giác AMC có : AB = AC do tam giác ABC cân tại A (gt)
góc ABC = góc ACB do tam giác ABC cân tại A (gT)
BM = MC do M là trđ của BC (gt)
=> tam giác AMB = tam giác AMC (c-g-c)
=> góc AMB = góc AMC (đn)
mà góc AMB + góc AMC = 180 (kb)
=> góc AMB = 90
=> AM _|_ BC (đn)
b, tam giác AMB = tam giác AMC (Câu b)
=> góc MAB = góc MAC (đn) mà AM nằm giữa AB và AC
=> AM là pg của góc BAC (đn)
A)VÌ \(\Delta ABC\)CÂN TẠI A
\(\Rightarrow\hept{\begin{cases}AB=AC\\\widehat{B}=\widehat{C}\end{cases}}\)
XÉT TAM GIÁC ABC
CÓ\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(đ/l\right)\)
THAY\(50^o+\widehat{B}+\widehat{C}=180^o\)
\(\widehat{B}+\widehat{C}=130^o\)
vì\(\widehat{B}=\widehat{C}\)
THAY \(\widehat{C}+\widehat{C}=130^o\)
\(2\widehat{C}=130^o\)
\(\widehat{C}=130^o:2=65^o\)
\(\Rightarrow\widehat{B}=\widehat{C}=65^o\)
B)XÉT\(\Delta BAM\)VÀ\(\Delta CAM\)CÓ
\(BA=CA\left(GT\right)\)
\(\widehat{B}=\widehat{C}\left(GT\right)\)
\(BM=CM\left(GT\right)\)
\(\Rightarrow\Delta BAM=\Delta CAM\left(C-G-C\right)\)
\(\Rightarrow\widehat{M_1}=\widehat{M_2}\)HAI GÓC TƯƠNG ỨNG
MÀ \(\widehat{M_1}+\widehat{M_2}=180^o\left(KB\right)\)
THAY\(\widehat{M_2}+\widehat{M_2}=180^o\)
\(2\widehat{M_2}=180^o\)
\(\widehat{M_2}=180^o:2=90^o\)
VẬY \(AM\perp BC\left(đpcm\right)\)
c) \(AM\perp BC\left(cmt\right)\)
=> AM LÀ ĐƯƠNG CAO CỦA TAM GIÁC ABC
TRONG TAM GIÁC CÂN ĐƯỜNG CAO CŨNG CHÍNH LÀ ĐƯỜNG PHÁP TUYẾN,PHÂN GIÁC,TRUNG TUYẾN
=> AM LÀ PHÂN GIÁC CỦA\(\widehat{BAC}\)
a) Xét \(\Delta ABC\)cân tại A có: \(\hept{\begin{cases}\widehat{B}=\widehat{C}\\\widehat{A}=50^o\end{cases}}\)
Mà \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(tính chất tổng 3 góc trong 1 tam giác)
\(\Rightarrow2\widehat{B}+50^o=180^o\)
\(\Rightarrow\widehat{A}=\frac{180^0-50^0}{2}=65^o\)
Cho ΔABC = ΔMNE, biết AB = 4cm, NE = 3cm, \(\widehat{A}\) = \(50^o\). Tính MN, BC, \(\widehat{M}\)
Mọi người giúp mình giải bài này với
MN=AB=4cm
NE=BC=3cm
\(\widehat{M}=\widehat{A}=50^0\)
Đúng 1
Bình luận (0)
Vì ΔABC = ΔMNE
nên:
+)MN=AB=4cm
+)NE=BC=3cm
+)góc A=góc M=50 độ
vậy:
+)MN=4cm
+)BC=3cm
+)góc M=50 độ
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(\widehat{A}=60^0;\widehat{C}=50^0\). Tia phân giác của góc B cắt AC ở D
Tính \(\widehat{ADB},\widehat{CDB}\) ?
Cho ΔABC vuông tại A (AB < AC)
Kẻ \(AH\perp BC\) tại H
a) Chứng minh \(\widehat{ABC}\) = \(\widehat{HAC}\)
b) Chứng minh \(\widehat{ACB}\) = \(\widehat{HAB}\)
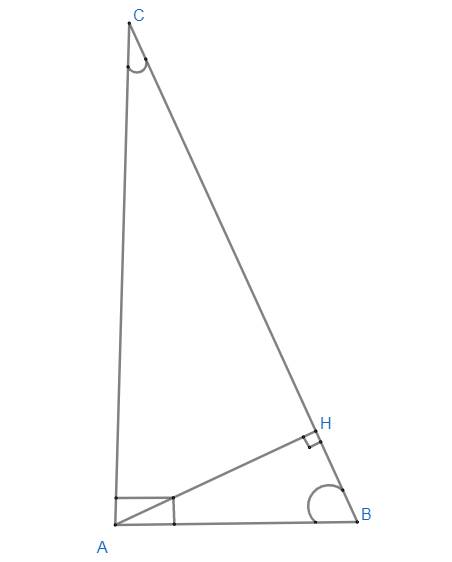
a)
Xét 2 tam giác vuông ABC và HAC có:
\(\widehat{C}\) chung
=> tg ABC \(\sim\) td HAC (g.g)
=> \(\widehat{ABC}=\widehat{HAC}\)
b)
Xét 2 tg vuông ACB và HAB có:
\(\widehat{B}\) chung
=> tg ACB \(\sim\) tg HAB (g.g)
=> \(\widehat{ACB}=\widehat{HAB}\)
Đúng 2
Bình luận (2)
Cho tam giác ABC có \(\widehat{B}=\widehat{C}=50^0.\) Gọi K là điểm trong tam giác sao cho \(\widehat{KBC}=10^0,\widehat{KCB=30^0.}\) CMR: tam giác ABK là tam giác cân và tính \(\widehat{BAK}\)
Cho tam giác ABC có \(\widehat{ABC}\)= \(50^0\),\(\widehat{BAC}=70^0\).Phân giác trong \(\widehat{ACB}\) cắt AB tại M.Trên MC lấy điểm N sao cho \(\widehat{MBN}=40^0\).Chứng minh BN=MC
Cho △ABC cân tại A; \(\widehat{BAC}=20^0\). Trên cạnh AC lấy điểm D sao cho \(\widehat{DBC}=50^0\); trên cạnh AB lấy điểm E sao cho \(\widehat{ECB}=60^0\). Tính \(\widehat{DEC}\)
giúp tui ik mn
cho \(\Delta ABC=\Delta MNQ\) biết \(\widehat {\rm{A}}={65^0}\) , \(\widehat {\rm{Q}}={50^0}\)
số đó góc B bằng :
Cho tam giac ABC có \(\widehat{B}\)= \(^{50^0}\). Trên tia đối của tia AB lấy điểm O . Trên nửa mặt phẳng không chứa C bờ AB vẽ \(\widehat{xOB}=50^o\)
a) Chứng minh Ox // BC
b) Qua A vẽ d // BC, chứng minh \(\widehat{ABC}+\widehat{BAC}+\widehat{ACB}=180^0\)



























