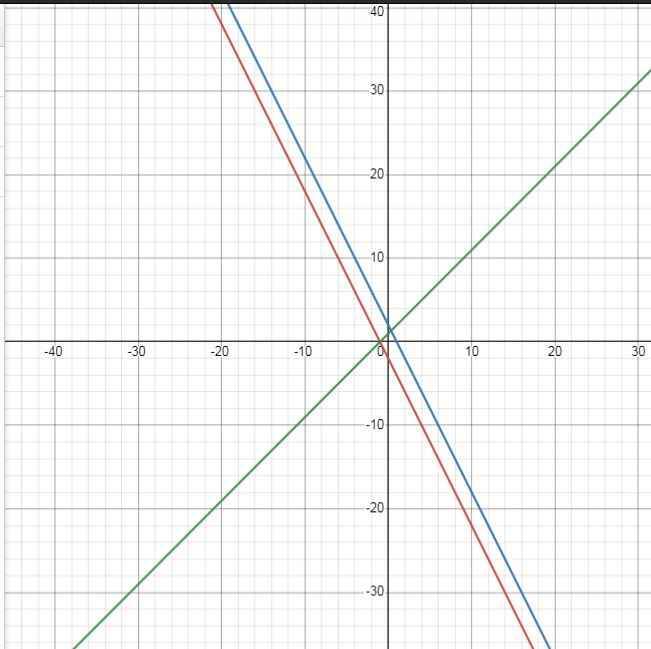
bài1: cho đường thẳng (d1)= 2x+2; (d2)y=\(\dfrac{-4}{3}\)x-2;(d3)y=\(\dfrac{1}{3}\)x+3
a)vẽ d1,d2,d3 trên cùng 1 hệ trục tọa độ
b)d2 và d3 giao Ox tại M và N. Tính Diện tích BMN
c)tính các góc tạo bởi 3 đường thẳng trên với trục Ox
Bài II (3,0 điểm) Cho 2 đường thẳng: (d1): y= +2x 4 và (d2): y=− +x 1 .
1) Tìm tọa độ giao điểm A của đường thẳng (d1) và đường thẳng (d2).
2) Xác định hệ số a, b của đường thẳng y ax b= + (a0) biết đường thẳng đó song song với đường thẳng (d1) và đi qua điểm M (-1; 3).
3) Gọi B và C lần lượt là giao điểm của đường thẳng (d1) và (d2) với trục hoành. Tính diện tích tam giác ABC.
1, PT hoành độ giao điểm: \(2x+4=-x+1\Leftrightarrow x=-1\Leftrightarrow y=0\)
\(\Leftrightarrow A\left(-1;0\right)\)
Vậy \(A\left(-1;0\right)\) là tọa độ giao điểm 2 đths
2, Đt cần tìm //(d1)\(\Leftrightarrow a=2;b\ne4\)
Đt cần tìm đi qua M(-1;3) nên \(-a+b=3\Leftrightarrow-2+b=3\Leftrightarrow b=5\left(tm\right)\)
Vậy đths là \(y=2x+5\)
3, PT giao điểm d1 với trục hoành là \(y=0\Leftrightarrow2x+4=0\Leftrightarrow x=-2\Leftrightarrow B\left(-2;0\right)\)
PT giao điểm d2 với trục hoành là \(y=0\Leftrightarrow-x+1=0\Leftrightarrow x=1\Leftrightarrow C\left(1;0\right)\)
Do đó \(BC=\left|-2\right|+\left|1\right|=3;OA=\left|-1\right|=1\)
Vậy \(S_{ABC}=\dfrac{1}{2}OA\cdot BC=\dfrac{3}{2}\left(đvdt\right)\)
Cho 2 đường thẳng: y= -3x -7 (d1) và y=2x+3 (d2)
Tìm tọa độ giao điểm M của hai đường thẳng (d1) , (d2)
Gọi \(A\left(x_0;y_0\right)\) là giao điểm \(\left(d_1\right)\) và \(\left(d_2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}y_0=-3x_0-7\\y_0=2x_0+3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_0=-\dfrac{4}{5}\\y_0=-\dfrac{23}{5}\end{matrix}\right.\)
\(\Rightarrow M\left(-\dfrac{4}{5};-\dfrac{23}{5}\right)\)
cho đường thẳng d1 : y = -2x+3 d2: y = -2x + m d3 : y = 1/2 x + 1 a) xét vị trí tương đối của hai đường thẳng d1 và d2 b) xét vị trí tương đối của hai đường thẳng d2 và d3
d1//d2 vì chung hệ số của x là -2
d2 cắt d3 do các hệ số a,b đều khác nhau
Cho 2 đường thẳng
(d1) y=x-7 (d2) y=-2x-1 viết phương trình đường thẳng (d) đi qua giao điểm của (d1) và (d2) đồng thời song song với đường thẳng x-2x+1
Cho các đường thẳng: d1:y=x+2,d2:y=5-2x,d3y=3x và d4:y=mx+m-5
a)Chứng minh rằng ba đường thẳng d1,d2,d3 đồng quy
b) Xác định m để ba đường thẳng d1,d2,d4 đồng quy
a) Phương trình hoành độ giao điểm của d₁ và d₂
x + 2 = 5 - 2x
⇔ x + 2x = 5 - 2
⇔ 3x = 3
⇔ x = 1
Thay x = 1 vào d₁ ta có:
y = 1 + 2 = 3
⇒ Giao điểm của d₁ và d₂ là A(1; 3)
Thay tọa độ điểm A vào d₃ ta có:
VT = 3
VP = 3.1 = 3
⇒ VT = VP
Hay A ∈ d₃
Vậy d₁, d₂ và d₃ đồng quy
b) Thay tọa độ điểm A(1; 3) vào d₄ ta có:
m.1 + m - 5 = 3
⇔ 2m - 5 = 3
⇔ 2m = 3 + 5
⇔ 2m = 8
⇔ m = 8 : 2
⇔ m = 4
Vậy m = 4 thì d₁, d₂ và d₄ đồng quy
Trong mặt phẳng Oxy cho 2 đường thẳng d1: 2x - y + 5=0, d2: 3x + 6y - 7=0. Lập phương trình đường thẳng đi qua P (2; -1) sao cho đường thẳng đó cắt d1, d2 tạo ra một tam giác cân có đỉnh là giao điểm của d1, d2
d1 có 1 vtpt là \(\overrightarrow{n1}\)(2;-1);d2 có 1 vtpt là \(\overrightarrow{n2}\)(3;6)
Ta có \(\overrightarrow{n1}\)\(\times\)\(\overrightarrow{n2}\)=2\(\times\)3-1\(\times\)6=0 nên d1 vuông góc d2 và d1 cắt d2 tại I(I khác P)
Gọi d là đườg thẳng đi qua P;d:A(x-2)+B(y+1)=0\(\Leftrightarrow\)Ax+By-2A+B=0
d cắt d1;d2 tạo thành một tam giác cân có đỉnh I\(\Leftrightarrow\)d tạo với d1(hoặc d2) một góc 45
\(\Leftrightarrow\)\(\frac{\left|2A-B\right|}{\sqrt{A^2+B^2}\sqrt{2^2+\left(-1\right)^2}}\)=\(\cos45\)
\(\Leftrightarrow\)\(3A^2\)-8AB-\(3B^2\)=0
\(\Leftrightarrow\)A=3B hoặc B=-3A
Nếu A=3B ta có d:3x+y-5=0
Nếu B=-3A to có d:x-3y-5=0
Vậy......
Cho đường thẳng (d1): y=-x+2 và đường thẳng (d2): y=2x+m-3. Xác định m để (d1) và (d2) tại điểm nằm trên trục hoành
Thay x=2 và y=0 vào (d2), ta được:
m+1=0
hay m=-1
1/Cho hai đường thẳng (d1):y = x + 4 và (d2):y = - 2x - 2 a) Vẽ đồ thị (d1) và (d2) trên cùng một mặt phẳng tọa độ. b) Cho đường thẳng (d3): y = ax + b . Xác định a và b biết đường thẳng (d3) song song với đường thẳng (d1) và (d3) cắt (d2)tại điểm A có hoành độ là -3.
\(b,\left(d_3\right)\text{//}\left(d_1\right)\Leftrightarrow\left\{{}\begin{matrix}a=1\\b\ne4\end{matrix}\right.\Leftrightarrow\left(d_3\right):y=x+b\)
PT hoành độ giao điểm \(\left(d_2\right);\left(d_3\right)\) là \(x+b=-2x-2\)
Mà 2 đt cắt tại hoành độ \(-3\) nên \(x=-3\)
\(\Leftrightarrow b-3=4\Leftrightarrow b=7\)
Vậy \(\left(d_3\right):y=x+7\)
Cho đường thẳng (d1): y=(m-1)x+m-2 và đường thẳng (d2): y=-2x+3. Tìm giá trị của m để hai đoạn thẳng (d1) và (d2) song song với nhau
Để (d1 ) và (d2 ) song song thì
+) b≠b'
⇔m-2≠3
⇔m≠5
+) a=a'
⇔m-1=-2
⇔m=-1 (thỏa mãn điều kiện)
Vậy tại m=-1 thì (d1) // (d2)
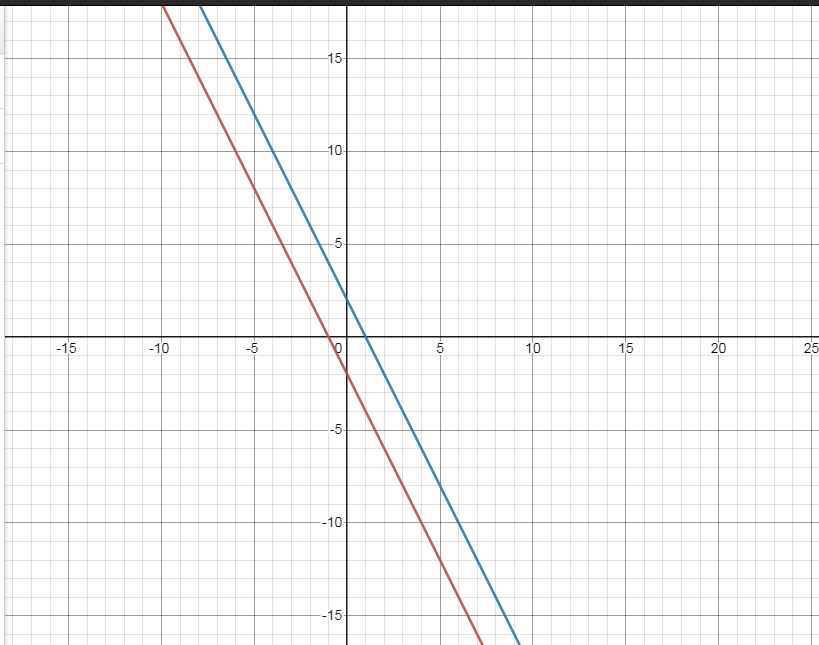
Cho hàm số y=-2x-2 có đồ thị là đường thẳng d1 A/ viết phương trình đường thẳng d2 biết rằng d2 đi qua điểm M (2;-2) và song song với đường thẳng d1 B/ vẽ d1 và d2 trên cùng một hệ trục tọa độ Oxy C/ cho hàm số y= x+m có đồ thị là đường thẳng d3, xác định tham số m để đường thẳng d1 cắt đường thẳng d3 trên trục Ox
a) \(\left(d_1\right):y=-2x-2\)
\(\left(d_2\right):y=ax+b\)
\(\left(d_2\right)//d_1\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b\ne-2\end{matrix}\right.\)
\(\Leftrightarrow\left(d_2\right):y=-2x+b\)
\(M\left(2;-2\right)\in\left(d_2\right)\Leftrightarrow-2.2+b=-2\)
\(\Leftrightarrow b=2\) \(\left(thỏa.đk.b\ne-2\right)\)
Vậy \(\left(d_2\right):y=-2x+2\)
b) \(\left\{{}\begin{matrix}\left(d_1\right):y=-2x-2\\\left(d_2\right):y=-2x+2\end{matrix}\right.\)
c) \(\left(d_3\right):y=x+m\)
\(\left(d_1\right)\cap\left(d_3\right)=A\left(x;0\right)\Leftrightarrow\left\{{}\begin{matrix}y=x+m\\y=-2x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}0=x+m\\0=-2x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\x=-1\end{matrix}\right.\)
\(\Rightarrow\left(d_3\right):y=x+1\)