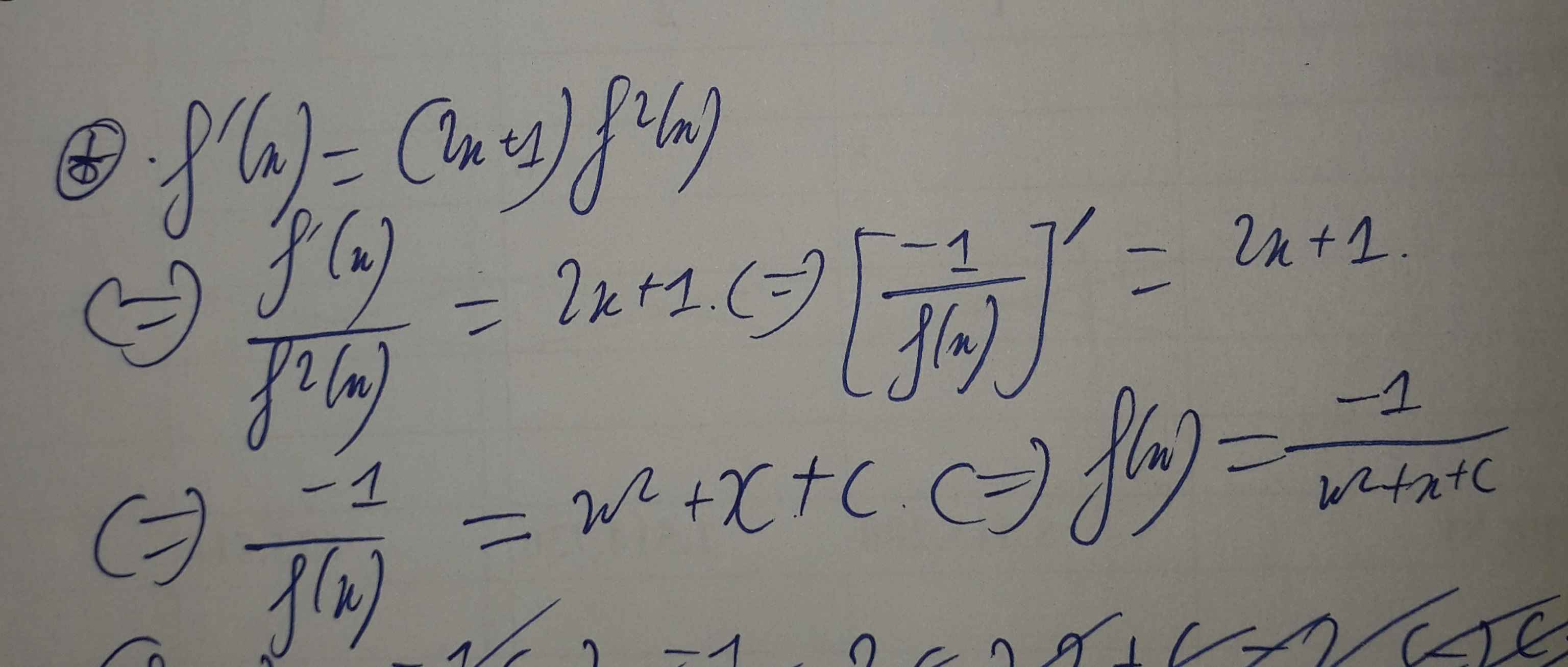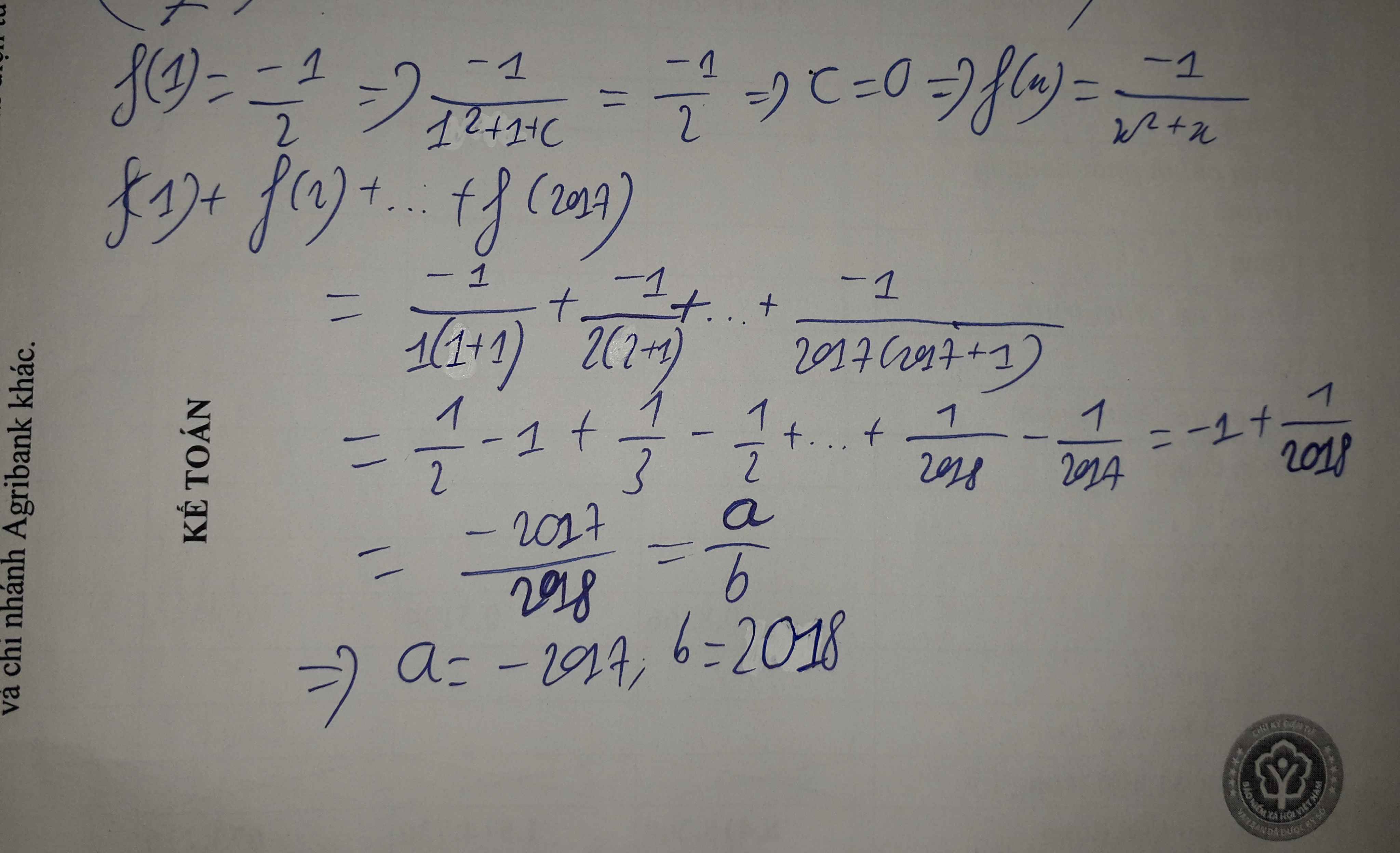Xác định a để \(f'\left(x\right)>0;\forall x\in R\) biết rằng \(f\left(x\right)=x^3+\left(a-1\right)x^2+2x+1\)

Những câu hỏi liên quan
a) Xác định a,b,c,d để đa thức\(f\left(x\right)=ax^4+bx^3+cx^2+dx+c\) thoả mãn điều kiện \(f\left(x\right)-f\left(x-1\right)=x^3\) với mọi x và f(0) = 0
Cho hàm số fleft(xright) xác định trên R, có đạo hàm fleft(xright)left(x^2-4right)left(x-5right)forall xin R và fleft(1right)0. Có bao nhiêu giá trị nguyên của tham số m để hàm số gleft(xright)left|fleft(x^2+1right)-mright| có nhiều điểm cực trị nhất?A.7 B. 8 C. 5 D. 6
Đọc tiếp
Cho hàm số \(f\left(x\right)\) xác định trên \(R\), có đạo hàm \(f'\left(x\right)=\left(x^2-4\right)\left(x-5\right)\forall x\in R\) và \(f\left(1\right)=0\). Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(g\left(x\right)=\left|f\left(x^2+1\right)-m\right|\) có nhiều điểm cực trị nhất?
A.7 B. 8 C. 5 D. 6

\(h\left(x\right)=f\left(x^2+1\right)-m\Rightarrow h'\left(x\right)=2x.f'\left(x^2+1\right)\)
\(h'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(x^2+1\right)=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x^2+1=2\\x^2+1=5\end{matrix}\right.\) \(\Rightarrow x=\left\{-2;-1;0;1;2\right\}\)
Hàm có nhiều cực trị nhất khi \(h\left(x\right)=m\) có nhiều nghiệm nhất
\(f\left(x\right)=\int f\left(x\right)dx=\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x+C\)
\(f\left(1\right)=0\Rightarrow C=-\dfrac{199}{12}\Rightarrow f\left(x\right)=-\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x-\dfrac{199}{12}\)
\(x=\pm2\Rightarrow x^2+1=5\Rightarrow f\left(5\right)\approx-18,6\)
\(x=\pm1\Rightarrow x^2+1=2\Rightarrow f\left(2\right)\approx6,1\)
\(x=0\Rightarrow x^2+1=1\Rightarrow f\left(1\right)=0\)
Từ đó ta phác thảo BBT của \(f\left(x^2+1\right)\) có dạng:

Từ đó ta dễ dàng thấy được pt \(f\left(x^2+1\right)=m\) có nhiều nghiệm nhất khi \(0< m< 6,1\)
\(\Rightarrow\) Có 6 giá trị nguyên của m
Đúng 1
Bình luận (2)
cho đa thức \(f\left(x\right)=ax^2+bx+c\)
a) xác định hệ số a,b,c biết \(f\left(0\right)=1;f\left(1\right)=0;f\left(-1\right)=10\)
b) tìm nghiệm của đa thức vừa xác định
Ta có: f(0)=1
<=> ax2 +bx+c=1
<=> c=1
f(1)=0
<=>ax2 +bx+c=0
<=> a+b+c=0
mà c=1
=>a+b=-1(1)
f(-1)=10
<=> ax2 +bx +c=10
<=>a-b+c=10
mà c=1
=>a-b=9(2)
Lấy (1) trừ (2) ta được (a+b)-(a-b)=-1-9
<=> 2b=-10
<=> b=-5
=>a=4
Vậy a=4,b=-5,c=1
Đúng 0
Bình luận (0)
xét đa thức :
a, \(f\left(x\right)=x^2+\left(a+b\right)x+ab\)và \(g\left(x\right)=x^2+5x+6\). xác định a ,b để f(x) = g(x)
b, \(f\left(x\right)=ãx^2+bx+c\)và \(g\left(x\right)=x\left(x+2\right)-\left(x+2\right)\). Xác định a , b để f(x)=g(x)
Cho hai hàm số f(x)=\(x^2\) và g(x)=3-x
a.tính f(-3), f\(\left(-\dfrac{1}{2}\right)\), f(0), g(1), g(2), g(3)
b,xác định a để 2f(a)=g(a)
b: Ta có: \(2\cdot f\left(a\right)=g\left(a\right)\)
\(\Leftrightarrow2a^2=3-a\)
\(\Leftrightarrow2a^2+a-3=0\)
\(\Leftrightarrow2a^2+3a-2a-3=0\)
\(\Leftrightarrow\left(2a+3\right)\left(a-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=1\\a=-\dfrac{3}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hàm số \(y=f\left(x\right)=ax\left(a\ne0\right)\) xác định với mọi \(x\in Q\)
Tìm giá rị của a để \(f\left(x_1\right)\cdot f\left(x_2\right)=f\left(x_1\cdot x_2\right)\)
Giúp mình với :3
\(f\left(x_1\right)=ax_1\) ; \(f\left(x_2\right)=ax_2\) ; \(f\left(x_1x_2\right)=ax_1x_2\)
Để \(f\left(x_1\right)f\left(x_2\right)=f\left(x_1x_2\right)\)
\(\Leftrightarrow ax_1.ax_2=ax_1x_2\)
\(\Leftrightarrow a^2x_1x_2=ax_1x_2\)
\(\Leftrightarrow a^2=a\)
\(\Leftrightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\a=1\end{matrix}\right.\)
Vậy \(a=1\)
Đúng 2
Bình luận (0)
Tìm m để các hàm số sau có tập xác định là R (hay luôn xác định trên R):
a. \(y=f\left(x\right)=\dfrac{3x+1}{x^2+2\left(m-1\right)x+m^2+3m+5}\)
b. \(y=f\left(x\right)=\sqrt{x^2+2\left(m-1\right)x+m^2+m-6}\)
c. \(y=f\left(x\right)=\dfrac{3x+5}{\sqrt{x^2-2\left(m+3\right)x+m+9}}\)
a.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+3m+5\ne0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+3m+5\right)< 0\)
\(\Leftrightarrow-5m-4< 0\)
\(\Leftrightarrow m>-\dfrac{4}{5}\)
b.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+m-6\ge0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+m-6\right)\le0\)
\(\Leftrightarrow-3m+7\le0\)
\(\Rightarrow m\ge\dfrac{7}{3}\)
c.
\(x^2-2\left(m+3\right)x+m+9>0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m+3\right)^2-\left(m+9\right)< 0\)
\(\Leftrightarrow m^2+5m< 0\Rightarrow-5< m< 0\)
Đúng 1
Bình luận (1)
Cho \(f\left(x\right)=ax^3+4x\left(x^2-1\right)+8\) và \(g\left(x\right)=x^3+4x\left(bx+1\right)+c-3\) xác định a, b, c để \(f\left(x\right)=g\left(x\right)\)
cho hàm số y = f(x) xác định và f(x) \(\ne0\) \(\forall x\in\left(0;+\infty\right)\), \(f'\left(x\right)=\left(2x+1\right)f^2\left(x\right)\) và f(1) = -1/2. Biết tổng f(1) + f(2) + f(3) + ... + f(2017) = a/b (a,b\(\in R\)) với a/b tối giản. Tìm a,b