Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính thể tích của hình nón có đỉnh là tâm O của hình vuông ABCD và đáy là hình tròn tiếp xúc với các cạnh của hình vuông A'B'C'D'. (H.10.38).
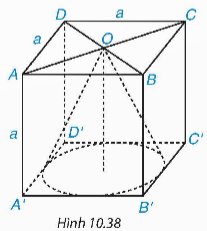
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính thể tích của hình nón có đỉnh là tâm O của hình vuông ABCD và đáy là hình tròn tiếp xúc với các cạnh của hình vuông A'B'C'D'. (H.10.38).

Bạn Khôi cho một hòn đá cảnh vào một bể nuôi cá hình trụ có đường kính đáy bằng 20 cm thì nước trong bể dâng lên 3 cm. Hỏi hòn đá cảnh đó có thể tích bằng bao nhiêu?
Thảo luận (1)Hướng dẫn giảiBể cá có bán kính đáy là: \(R = \frac{{20}}{2} = 10cm\).
Thể tích nước dâng lên là: \(V = \pi {.10^2}.3 = 300\pi \left( {c{m^3}} \right)\).
Vì thể tích hòn đá chính bằng thể tích nước dâng lên nên thể tích hòn đá bằng \(300\pi \;c{m^3}\).
(Trả lời bởi datcoder)
Một chiếc kem ốc quế gồm hai phần: Phần phía dưới dạng hình nón có chiều cao gấp đôi bán kính đáy, phần trên là nửa hình cầu có đường kính bằng đường kính đáy của hình nón phía dưới (H.10.39). Thể tích phần kem phía trên bằng 200 cm3. Tính thể tích của cả chiếc kem.
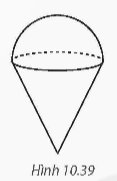
Thảo luận (1)Hướng dẫn giảiGọi bán kính đáy của hình nón là R. Khi đó, chiều cao của hình nón là 2R, hình cầu có bán kính là R.
Thể tích phần kem phía trên là \(200c{m^3}\) nên ta có:
\(\frac{1}{2}.\frac{4}{3}\pi {R^3} = 200\) nên \(\frac{2}{3}\pi {R^3} = 200\)
Thể tích hình nón phía dưới là:
\(\frac{1}{3}\pi {R^2}.2R = \frac{2}{3}\pi {R^3} = 200\left( {c{m^3}} \right)\).
Thể tích của cả chiếc kem là:
\(200 + 200 = 400\left( {c{m^3}} \right)\).
(Trả lời bởi datcoder)
Mái nhà hát Cao Văn Lầu và Trung tâm triển lãm Văn hóa Nghệ thuật tỉnh Bạc Liêu có hình dáng ba chiếc nón lá lớn nhất Việt Nam (H.10.40). Tính diện tích một mái nhà hình nón có đường kính bằng 45 m và chiều cao bằng 24 m (làm tròn kết quả đến hàng đơn vị của m2).

Thảo luận (1)Hướng dẫn giảiBán kính đáy mái nhà là: \(R = \frac{{45}}{2}m\).
Độ dài đường sinh mái nhà là:
\(l = \sqrt {{{\left( {\frac{{45}}{2}} \right)}^2} + {{24}^2}} = \frac{{3\sqrt {481} }}{2}\left( m \right)\).
Diện tích một mái nhà là:
\(S = \pi Rl = \pi .\frac{{45}}{2}.\frac{{3\sqrt {481} }}{2} \approx 2325\left( {{m^2}} \right)\).
(Trả lời bởi datcoder)