Một số họa tiết và hoa văn trên thổ cẩm (Hình 64) có dạng hình vuông
Hình vuông có những tính chất gì? Có những dấu hiệu nào để nhận biết một tứ giác là hình vuông?
Bài 7. Hình vuông
Khởi động (SGK Cánh Diều trang 116)
Thảo luận (1)
Hoạt động 1 (SGK Cánh Diều trang 116)
Cho biết các góc và các cạnh của tứ giác ABCD ở Hình 65 có đặc điểm gì?
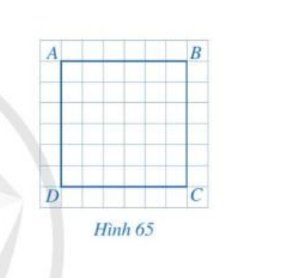
Thảo luận (1)Hướng dẫn giảiDo tứ giác ABCD là hình vuông nên các cạnh AB, BC, CD, DA bằng nhau và các góc \(\widehat{ABC},\widehat{BCD},\widehat{CDA},\widehat{DAB}\) bằng nhau và bằng 90o.
(Trả lời bởi Hà Quang Minh)
Hoạt động 2 (SGK Cánh Diều trang 117)
a) Mỗi hình vuông có là một hình chữ nhật hay không?
b) Mỗi hình vuông có là một hình thôi hay không?
Thảo luận (1)Hướng dẫn giảia) Mỗi hình vuông có là hình chữ nhật vì có 4 góc bằng nhau và bằng 90o
b) Mỗi hình vuông có là một hình thoi vì có các cạnh bằng nhau
(Trả lời bởi Hà Quang Minh)
Luyện tập 1 (SGK Cánh Diều trang 117)
Cho hình vuông ABCD. Tính số đo các góc CAB, DAC.
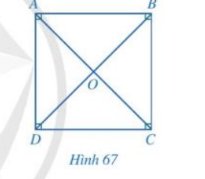
Thảo luận (1)Hướng dẫn giảiDo tứ giác ABCD là hình vuông \(\Rightarrow\widehat{CAB}=\widehat{DAC}=\dfrac{\widehat{BAD}}{2}=\dfrac{90^o}{2}=45^o\)
(Trả lời bởi Hà Quang Minh)
Hoạt động 3 (SGK Cánh Diều trang 118)
a) Cho hình chữ nhật ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình vuông hay không?b) Cho hình chữ nhật ABCD có hai đường chéo AC và BD vuông góc với nhau (hình 69).- Đường thẳng có phải là đường trung trực của đoạn thẳng BD hay không?c) Cho hình chữ nhật ABCD có AC là tia phân giác của góc DAB- Tam giác ABC có phải là tam giác vuông cân hay không?ABCD có phải là hình vuông hay không?
Đọc tiếp
a) Cho hình chữ nhật ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình vuông hay không?
b) Cho hình chữ nhật ABCD có hai đường chéo AC và BD vuông góc với nhau (hình 69).
- Đường thẳng có phải là đường trung trực của đoạn thẳng BD hay không?
c) Cho hình chữ nhật ABCD có AC là tia phân giác của góc DAB
- Tam giác ABC có phải là tam giác vuông cân hay không?
ABCD có phải là hình vuông hay không?
Thảo luận (1)Hướng dẫn giảia, Hình chữ nhật ABCD có AB = BC
Suy ra hình chữ nhật ABCD có \(\widehat A = \widehat B = \widehat C = \widehat D = {90^0};AB = BC = CD = DA\)
Suy ra hình chữ nhật ABCD là hình vuông
b, O là giao điểm của AC và BD.
Vì ABCD là hình chữ nhật nên OB = OD.
Mà AC vuông góc BD. Suy ra AC là đường trung trực của đoạn thẳng BD.
Xét \(\Delta ABD\) có AO vừa là đường trung trực vừa là đường cao
\( \Rightarrow \Delta ABD \) là tam giác vuông cân tại A.
\( \Rightarrow AB = AD\)
Mà AB = CD, AD = BC (tính chất hình chữ nhật)
\(\Rightarrow AB = BC = CD = DA\) nên ABCD là hình vuông.
c, Ta có ABCD là hình chữ nhật nên \(\widehat A =\widehat B = \widehat C = \widehat D = 90^0\)
Vì AC là tia phân giác của góc DAB nên ta có: \(\widehat{DAC} = \widehat{CAB} =\frac{\widehat{DAB}}{2} = \frac{90^0}{2} = 45^0\)
Xét tam giác ABC vuông tại B (\(\widehat B = 90^0\)), ta có:
\(\widehat{ACB} + \widehat B + \widehat{CAB} = 180^0\)
\(\Rightarrow \widehat{ACB} = 180^0 - \widehat B - \widehat{CAB} = 180^0 - 90^0 - 45^0 = 45^0\)
\( \Rightarrow \widehat{ACB} = \widehat{CAB} =45^0\) nên tam giác ABC vuông cân tại B.
\( \Rightarrow AB = BC\)
Mà AB = CD, BC = AD (tính chất hình chữ nhật)
\(\Rightarrow AB = BC = CD = DA\) nên ABCD là hình vuông.
(Trả lời bởi Hà Quang Minh)
Luyện tập 2 (SGK Cánh Diều trang 118)
Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy điểm D, E sao cho: BD = DE = EC
Qua D và E kẻ đường thẳng vuông góc với BC, chúng cắt AB và AC lần lượt tại H và G. Chứng minh tứ giác DEGH là hình vuông.
Thảo luận (1)Hướng dẫn giảiXét \(\Delta ABC\) vuông cân tại A
\( \Rightarrow \widehat {ABC} = \widehat {ACB} = {45^0}\)
Xét \(\Delta HDB\) vuông tại D có: \(\widehat {DBH} = \widehat {ABC} = {45^0}\)
\(\begin{array}{l} \Rightarrow \widehat {BHD} = {90^0} - \widehat {DBH} = {90^0} - {45^0} = {45^0}\\ \Rightarrow \widehat {BHD} = \widehat {DBH} = {45^0}\end{array}\)
\( \Rightarrow \Delta HDB\)vuông cân tại D suy ra DB = DH (1)
Xét \(\Delta EGC\)vuông tại E có \(\widehat {ECG} = \widehat {BCA} = {45^0}\)
\(\begin{array}{l} \Rightarrow \widehat {CGE} = {90^0} - \widehat {ECG} = {90^0} - {45^0} = {45^0}\\ \Rightarrow \widehat {CGE} = \widehat {ECG} = {45^0}\end{array}\)
\( \Rightarrow \Delta EGC\)vuông cân tại E suy ra EC = EG (2)
Theo đề bài: BD = DE = EC (3)
Từ (1), (2), (3) suy ra: HD = DE =EG.
Xét tứ giác HDEG có HD//EG (vì cùng vuông góc với BC) HD = EG
Suy ra tứ giác HDEG là hình bình hành mà : \(\widehat {HDE} = {90^0}\)
Suy ra hình bình hành HDEG là hình chữ nhật.
Mặt khác: HD =DE. Suy ra hình chữ nhật HDEG là hình vuông
(Trả lời bởi Hà Quang Minh)
Bài 1 (SGK Cánh Diều trang 119)
Cho hình thoi ABCD có AC = BD. Chứng minh ABCD là hình vuông.
Thảo luận (2)Hướng dẫn giải
Bài 2 (SGK Cánh Diều trang 119)
Cho hình thoi ABCD có \(\widehat A = {90^o}\). Chứng minh ABCD là hình vuông.
Thảo luận (2)Hướng dẫn giải
Bài 3 (SGK Cánh Diều trang 119)
Cho tam giác ABC vuông tại A có đường phân giác AD. Gọi H, K lần lượt là hình chiếu của D trên AB, AC. Chứng minh tứ giác AHDK là hình vuông.
Thảo luận (1)Hướng dẫn giảiXét tứ giác AHDK có: \(\widehat A = \widehat H = \widehat K = {90^0}\)
Suy ra tứ giác AHDK là hình chữ nhật
Mà: AD là tia phân giác của \(\widehat {HAK}\)
Suy ra hình chữ nhật AHDK là hình vuông
(Trả lời bởi Hà Quang Minh)
Bài 4 (SGK Cánh Diều trang 119)
Cho hai mảnh giấy, mỗi mảnh có dạng hình vuông với độ dài 1dm. Hãy trình bày cách cắt ghép hai mảnh giấy đó để được một hình vuông có độ dài cạnh là \(\sqrt 2 dm\).
Thảo luận (1)Hướng dẫn giảiGiả sử có hai hình vuông ABCD và EFGH có độ dài 1 dm. Khi đó các đường chéo của hai hình vuông có độ dài \(\sqrt 2 dm\).
Bước 1: Cắt theo đường chéo theo đường chéo AC ta được hai mảnh tam giác có độ dài cạnh lớn nhất là \(\sqrt 2 dm\).
Bước 2: Cắt theo đường chéo theo đường chéo EG ta được hai mảnh tam giác có độ dài cạnh lớn nhất là \(\sqrt 2 dm\).
Bước 3: Ghép 4 hình tam giác sao cho cạnh lớn nhất là cạnh của hình vuông ta được hình vuông có độ dài cạnh là \(\sqrt 2 dm\)
(Trả lời bởi Hà Quang Minh)