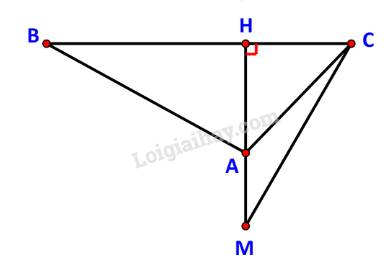
Một tàu đánh cá xuất phát từ cảng A, đi theo hướng \(S{70^o}E\) với vận tốc 70 km/h. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam với vận tốc 8 km/h. Sau 2 giờ kể từ khi động cơ bị hỏng, tàu neo đậu được vào một hòn đảo.
a) Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu.
b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.