Màn hình phẳng của chiếc ti vi ở Hình 46 có dạng hình chữ nhật.
Hình chữ nhật có những tính chất gì? Có những dấu hiệu nào để nhận biết một tứ giác là hình chữ nhật?
Bài 5. Hình chữ nhật
Khởi động (SGK Cánh Diều trang 109)
Thảo luận (1)
Hoạt động 1 (SGK Cánh Diều trang 109)
Cho biết số đo mỗi góc của tứ giác ABCD ở Hình 47.
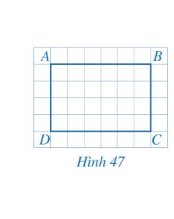
Thảo luận (1)Hướng dẫn giảiTứ giác ABCD có: \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)
(Trả lời bởi Hà Quang Minh)
Hoạt động 2 (SGK Cánh Diều trang 109)
a) Mỗi hình chữ nhật có là một hình thang cân hay không?
b) Mỗi hình chữ nhật có là một hình bình hành hay không?
Thảo luận (1)Hướng dẫn giảia) Một hình chữ nhật là một hình thang cân
b) Một hình chữ nhật là một hình bình hành
(Trả lời bởi Hà Quang Minh)
Luyện tập 1 (SGK Cánh Diều trang 110)
Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N lần lượt là hình chiếu của O trên AB, BC. Chứng minh: \(MN = \dfrac{1}{2}AC\).
Thảo luận (1)Hướng dẫn giảiDo ABCD là hình chữ nhật, O là giao điểm của AC và BD
Suy ra OA = OB = OC = OD.
Xét tứ giác MBNO có:
\(\widehat M = \widehat N = {90^0}\) (Do M, N lần lượt là hình chiếu của O trên AB, BC)
\(\widehat B = {90^0}\)
nên MBNO là hình chữ nhật.
Suy ra MN = BO (tính chất hai đường chéo của hình chữ nhật)
\( MN = \dfrac{1}{2}AC\) (do \(BO = AO = OC = \dfrac{1}{2}AC\))
(Trả lời bởi Hà Quang Minh)
Hoạt động 3 (SGK Cánh Diều trang 110)
a) Cho hình bình hành ABCD có widehat A {90^o}. ABCD có phải là hình chữ nhật hay không?b) Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau (hình 50).Hai tam giác ABC và DCB có bằng nhau hay không? Từ đó, hãy so sánh widehat {ABC} và widehat {DCB}.ABCD có phải là hình chữ nhật hay không?
Đọc tiếp
a) Cho hình bình hành ABCD có \(\widehat A = {90^o}\). ABCD có phải là hình chữ nhật hay không?
b) Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau (hình 50).
Hai tam giác ABC và DCB có bằng nhau hay không? Từ đó, hãy so sánh \(\widehat {ABC}\) và \(\widehat {DCB}\).
ABCD có phải là hình chữ nhật hay không?
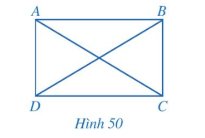
Thảo luận (1)Hướng dẫn giảia) Hình bình hành ABCD có \(\widehat A = {90^o}\)
Suy ra: \(\widehat C = \widehat A = {90^o}\)
Suy ra: \(\widehat B = \widehat D = \dfrac{{{{360}^o} - \widehat A - \widehat C}}{2} = \dfrac{{{{360}^o} - {{90}^o} - {{90}^o}}}{2} = {90^o}\)
Vậy ABCD là hình chữ nhật
b) Xét hai tam giác ABC và tam giác DCB có:
BC chung
AB = DC
AC = BD
Suy ra: \(\Delta ABC = \Delta DCB \Rightarrow \widehat {ABC} = \widehat {DCB}\)
Suy ra: \(\widehat {ABC} = \widehat {DCB} = \widehat {ADC} = \widehat {DAB} = {360^o}:4 = {90^o}\)
Vậy ABCD là hình chữ nhật.
(Trả lời bởi Hà Quang Minh)
Luyện tập 2 (SGK Cánh Diều trang 111)
Cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O thỏa mãn \(\widehat {OAB} = \widehat {O{\rm{D}}C}\). Chứng minh ABCD là hình chữ nhật.
Thảo luận (1)Hướng dẫn giảiDo ABCD là hình bình hành suy ra AB = CD và AB // CD nên \(\widehat{ABO}=\widehat{ODC}\) (hai góc so le trong\)
Mà \(\widehat {OAB} = \widehat {O{\rm{D}}C}\) nên \(\widehat{ABO}=\widehat{OAB}\) suy ra tam giác AOB cân tại O.
Vì tam giác AOB cân tại O nên OA = OB.
Mà hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường nên AC = BD.
Suy ra ABCD có hai đường chéo AC = BD nên ABCD là hình chữ nhật.
(Trả lời bởi Hà Quang Minh)
Bài 1 (SGK Cánh Diều trang 111)
Cho hình thang cân ABCD có AB // CD, \(\widehat A = {90^o}\). Chứng minh ABCD là hình chữ nhật.
Thảo luận (2)Hướng dẫn giải
Bài 2 (SGK Cánh Diều trang 111)
Cho tam giác ABC vuông tại A có M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh tứ giác ABCD là hình chữ nhật và \(AM = \dfrac{1}{2}BC\).
Thảo luận (1)Hướng dẫn giảiXét tứ giác ABCD có:
MB = MC (M là trung điểm của BC)
MA = MD (gt)
Suy ra tứ giác ABDC là hình bình hành (có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Mà hình bình hành ABDC có \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over A} = {90^0}\)nên ABCD là hình chữ nhật
Vì: ABDC là hình chữ nhật nên BC = AD
Mà: \(AM = \dfrac{1}{2}AC = \dfrac{1}{2}BC\)
(Trả lời bởi Hà Quang Minh)
Bài 3 (SGK Cánh Diều trang 111)
Cho hình chữ nhật ABCD có điểm E nằm trên cạnh CD sao cho \(\widehat {A{\rm{E}}B} = {78^o};\widehat {EBC} = {39^o}\). Tính số đo của \(\widehat {BEC}\) và \(\widehat {E{\rm{A}}B}\).
Thảo luận (1)Hướng dẫn giảiXét tam giác BEC vuông tại C có:
\(\begin{array}{l}\widehat {BEC} + \widehat {EBC} + \widehat {BCE} = {180^o}\\ \Rightarrow \widehat {BEC} + {39^o} + {30^o} = {180^o}\\ \Rightarrow \widehat {BEC} = {180^o} - {39^o} - {30^o} = {51^o}\end{array}\)
Mà: \(\begin{array}{l}\widehat {EBA} + \widehat {EBC} = {90^o}\\ \Rightarrow \widehat {EBA} = {90^o} - \widehat {EBC} = {90^o} - {39^o} = {51^o}\end{array}\)
Xét tam giác AEB có:
\(\begin{array}{l}\widehat {A{\rm{E}}B} + \widehat {E{\rm{A}}B} + \widehat {EBA} = {180^o}\\ \Rightarrow \widehat {E{\rm{A}}B} = {180^o} - \widehat {A{\rm{E}}B} - \widehat {EBA} = {180^o} - {78^o} - {51^o} = {51^o}\end{array}\)
(Trả lời bởi Hà Quang Minh)
Bài 4 (SGK Cánh Diều trang 111)
Một khu vườn có dạng tứ giác ABCD với các góc A, B, D là góc vuông, AB = 400 m, AD = 300 m. Người ta đã làm một cái hồ nước có dạng hình tròn, khi đó vị trí C không còn nằm trong khu vườn nữa (hình 52). Tính khoảng cách từ vị trí C đến mỗi vị trí A, B, D.
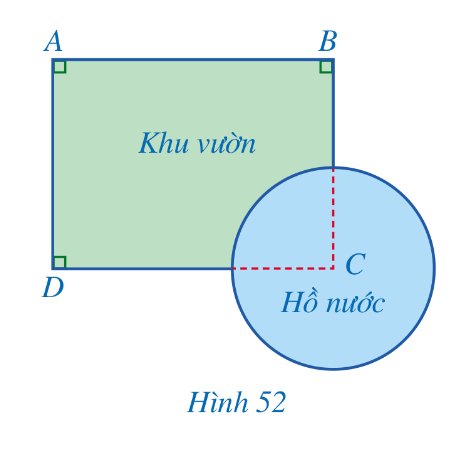
Thảo luận (1)Hướng dẫn giảiTứ giác ABCD có các góc A, B, D là góc vuông nên tứ giác ABCD là hình chữ nhật
Khi đó: CD = AB = 400 m
CB = AD = 300
Xét tam giác vuông ABC vuông tại B ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} = {400^2} + {300^2} = 250000\\ \Rightarrow AC = 500\end{array}\)
Vậy khoảng cách từ C đến mỗi vị trí A, B, D lần lượt là: 500m; 300m; 400m.
(Trả lời bởi Hà Quang Minh)