Nêu một số đồ vật có dạng hình trụ trong đời sống.
Bài 31. Hình trụ và hình nón
Câu hỏi (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 94)
Thảo luận (1)
Luyện tập 1 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 94)
Kể tên các bán kính đáy và đường sinh còn lại của hình trụ có trong Hình 10.4.
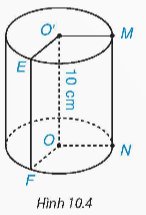
Thảo luận (1)Hướng dẫn giảiTrong Hình 10.4, ta có:
− Các bán kính đáy còn lại của hình trụ là: ON, OF, O'E.
− Đường sinh còn lại của hình trụ là: MN.
(Trả lời bởi datcoder)
Thực hành 1 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 95)
Chuẩn bị một băng giấy cứng hình chữ nhật ABCD với AB = 8 cm, BC = 15 cm. Cuộn băng giấy lại sao cho hai cạnh AB và DC sát vào nhau như Hình 10.6 (dùng băng keo dán), ta được một hình trụ (không có đáy). Hãy cho biết chiều cao và chu vi đáy của hình trụ đó.
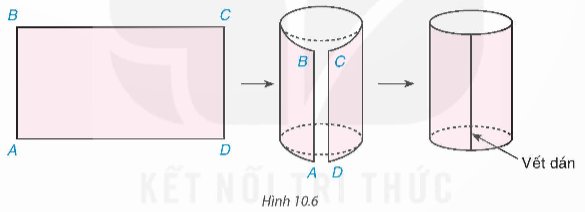
Thảo luận (1)Hướng dẫn giảiChiều cao của hình trụ đó chính là đoạn thẳng AB nên chiều cao bằng 8 cm.
Vì băng giấy được cuộn vào nên ta được hai đáy tạo thành các hình tròn, nên chu vi hình tròn là đoạn thẳng BC. Do đó chu vi đáy của hình trụ bằng 15 cm.
(Trả lời bởi datcoder)
Hoạt động 1 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 95)
Người ta coi diện tích hình chữ nhật ABCD chính là diện tích xung quanh của hình trụ được tạo thành (xem Thực hành 1). Cho hình trụ có chiều cao h = 9 cm và bán kính đáy R = 5 cm. Tính diện tích mặt xung quanh của hình trụ.
Thảo luận (1)Hướng dẫn giảiHình chữ nhật ABCD có một cạnh bằng chu vi hình tròn đáy, cạnh còn lại bằng chiều cao của hình trụ.
Nên ta có một cạnh của hình chữ nhật bằng 9cm.
Cạnh còn lại của hình chữ nhật (hay chu vi hình tròn đáy) là:
\(2.\pi .R = 2.\pi .5 = 10\pi \)
Diện tích hình chữ nhật ABCD là: \(10\pi .9 = 90\pi \left( {c{m^2}} \right)\).
Do đó, diện tích xung quanh của hình trụ là \(90\pi c{m^2}\).
(Trả lời bởi datcoder)
Hoạt động 2 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 95)
Hãy nhắc lại công thức tính thể tích của hình lăng trụ đứng tam giác (hoặc hình lăng trụ đứng tứ giác) có diện tích đáy S và chiều cao h.
Thảo luận (1)Hướng dẫn giảiCông thức tính thể tích hình lăng trụ đứng tam giác(hoặc hình lăng trụ đứng tứ giác) là:
V=S.h
(Trả lời bởi RAVG416)
Luyện tập 2 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 96)
Một thùng nước có dạng hình trụ với chiều cao bằng 1,6 m và bán kính đáy bằng 0,5 m.
a) Tính diện tích xung quanh của thùng nước.
b) Hỏi thùng chứa được bao nhiêu lít nước?
(Coi chiều dày của thùng không đáng kể và làm tròn kết quả ở câu b đến hàng đơn vị của lít).
Thảo luận (1)Hướng dẫn giảia) Diện tích xung quanh của thùng nước là: \({S_{xq}} = 2.\pi .0,5.1,6 = 1,6\pi \left( {{m^2}} \right)\).
b) Thể tích của thùng nước là: \(V = \pi .0,{5^2}.1,6 = 0,4\pi \approx 1,257\left( {{m^3}} \right)\)
Đổi \(1,257{m^3} = 1\;257\left( l \right)\)
Vậy thùng nước chứa được khoảng 1 257 lít nước.
(Trả lời bởi datcoder)
Câu hỏi (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 97)
Nêu một số đồ vật có dạng hình trụ trong đời sống.
Thảo luận (1)Hướng dẫn giải1.Lon nước ngọt: Thường có dạng hình trụ tròn đứng.
2.Ống nước: Dùng trong xây dựng và dẫn nước.
3.Ly cốc: Nhiều loại ly, cốc uống nước có dạng hình trụ.
4.Pin tiểu: Các loại pin AA, AAA có hình trụ.
5.Thùng phi: Thùng chứa xăng dầu, hóa chất thường có dạng hình trụ lớn.
6.Chai nước: Nhiều loại chai nước cũng có hình trụ ở phần thân.
7.Cuộn giấy vệ sinh: Có lõi bên trong dạng hình trụ.
(Trả lời bởi RAVG416)
Luyện tập 3 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 98)
Kể tên các bán kính đáy và các đường sinh còn lại của hình nón trong Hình 10.10.
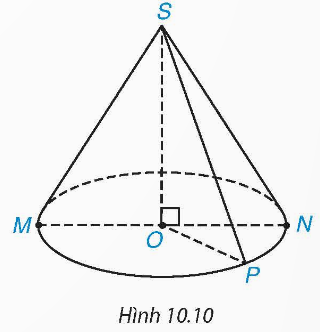
Thảo luận (1)Hướng dẫn giảiON, OP là các bán kính đáy của hình nón.
SP, SN là các đường sinh của hình nón.
(Trả lời bởi datcoder)
Thực hành 2 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 98)
Cắt một nửa hình tròn bằng giấy cứng, có đường kính AB = 20 cm và tâm là S. Cuộn nửa hình tròn đó lại sao cho SA và SB sát vào nhau như Hình 10.12 (dùng băng keo dán), ta được một hình nón đỉnh S. Hãy cho biết độ dài đường sinh và chu vi đáy của hình nón đó.
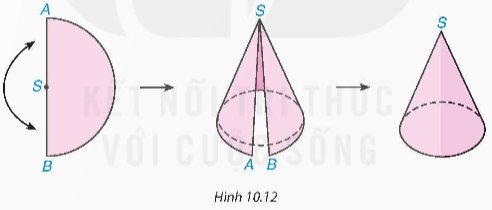
Thảo luận (1)Hướng dẫn giảiTa có đường sinh của hình nón là đoạn thẳng SA nên độ dài đường sinh là \(\frac{1}{2}.20 = 10\) (cm).
Vì hình nón được tạo bởi nửa hình tròn nên chu vi đáy của hình nón chính là độ dài cung AB hay nửa chu vi của hình tròn đường kính AB.
Chu vi hình tròn đáy của hình nón là: \(\frac{{20\pi }}{2} = 10\pi \) (cm).
(Trả lời bởi datcoder)
Hoạt động 3 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 98)
Người ra coi diện tích của hình quạt tròn SAB (xem Thực hành 2) chính là diện tích xung quanh của hình nón được tạo thành. Cho hình nón có đường sinh ℓ = 9 cm và bán kính đáy r = 5 cm. Tính diện tích mặt xung quanh của hình nón.

Thảo luận (1)Hướng dẫn giảiVì bán kính đáy của hình nón là r = 5cm nên ta có độ dài cung AB chính là chu vi của hình tròn bán kính 5cm.
Do đó độ dài cung AB là:
\(2r\pi = 2.5.\pi = 10\pi \left( {cm} \right)\)
Diện tích hình quạt có độ dài cung tròn là \(10\pi \) và bán kính R là 9 là:
\({S_q} = \frac{{10\pi .9}}{2} = 45\pi \left( {c{m^2}} \right)\)
Vậy diện tích mặt xung quanh của hình nón là \(45\pi c{m^2}\).
(Trả lời bởi datcoder)