Hãy nhắc lại công thức tính thể tích của hình chóp tam giác đều (hoặc hình chóp tứ giác đều) có diện tích đáy S và chiều cao h.
Bài 31. Hình trụ và hình nón
Hoạt động 4 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 99)
Thảo luận (1)
Luyện tập 4 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 99)
Tính diện tích xung quanh và thể tích của một hình nón có độ dài đường sinh bằng 13 cm và chiều cao bằng 12 cm.
Thảo luận (1)Hướng dẫn giải
Xét hình nón có đường sinh \(CB = 13cm\) và chiều cao \(CA = 12cm\).
Tam giác CAB vuông tại A nên
\(C{A^2} + A{B^2} = C{B^2}\)
\({12^2} + A{B^2} = {13^2}\)
\(AB = 5cm\)
Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi .BA.CB = 5.13.\pi = 65\pi \left( {c{m^2}} \right)\).
Thể tích của hình nón là:
\(V = \frac{1}{3}\pi .A{B^2}.CA = \frac{1}{3}{.5^2}.12.\pi = 100\pi \left( {c{m^3}} \right)\).
(Trả lời bởi datcoder)
Vận dụng (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 99)
Người ta đổ muối thu hoạch được trên cánh đồng muối thành từng đống có dạng hình nón với chiều cao khoảng 0,9 m và đường kính đáy khoảng 1,6 m. Hỏi mỗi đống muối có bao nhiêu decimét khối muối? (Làm tròn kết quả đến hàng đơn vị của dm3).
Thảo luận (1)Hướng dẫn giảiBán kính đống muối là:
\(r = \frac{{1,6}}{2} = 0,8\left( m \right)\).
Mỗi đống muối có số đềximét khối là:
\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .0,{8^2}.0,9 \approx 0,603\left( {{m^3}} \right) = 603d{m^3}\)
(Trả lời bởi datcoder)
Bài tập 10.1 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 100)
Thay dấu “?” bằng giá trị thích hợp và hoàn thành bảng sau vào vở:
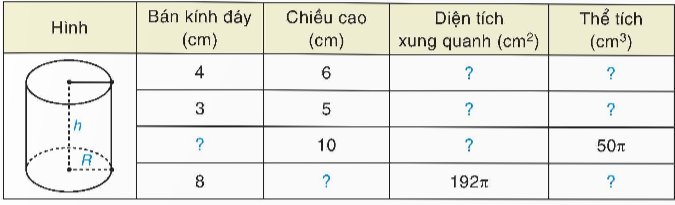
Bài tập 10.2 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 100)
Cho hình chữ nhật ABCD có AB = 3 cm, BC = 4 cm. Quay hình chữ nhật quanh cạnh AB một vòng, ta được một hình trụ. Tính diện tích xung quanh và thể tích của hình trụ tạo thành.
Thảo luận (1)Hướng dẫn giảiKhi quay hình chữ nhật quanh cạnh AB một vòng, ta được một hình trụ có chiều cao \(h = 3cm\) và bán kính \(R = 4cm\).
Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi Rh = 2\pi .4.3 = 24\pi \left( {c{m^2}} \right)\).
Thể tích của hình trụ là:
V = Sđáy.h\( = \pi {R^2}h\)\( = \pi {.4^2}.3 = 48\pi \left( {c{m^3}} \right)\)
(Trả lời bởi datcoder)
Bài tập 10.3 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 100)
Khi cho tam giác SOA vuông tại O quay quanh cạnh SO một vòng, ta được một hình nón. Biết OA = 8 cm, SA = 17 cm (H.10.14).
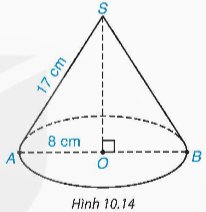
a) Tính diện tích xung quanh của hình nón.
b) Tính thể tích của hình nón.
Thảo luận (1)Hướng dẫn giảia) Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi .OA.SA = \pi .8.17 = 136\pi \left( {c{m^2}} \right)\)
b) Áp dụng định lí Pythagore vào tam giác SAO vuông tại O có: \(S{O^2} + A{O^2} = S{A^2}\)
\(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{{17}^2} - {8^2}} = 15\left( {cm} \right)\)
Thể tích của hình nón là:
\(V = \frac{1}{3}\pi .A{O^2}.SO = \frac{1}{3}\pi {.8^2}.15 = 320\pi \left( {c{m^3}} \right)\).
(Trả lời bởi datcoder)
Bài tập 10.4 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 100)
Một bóng đèn huỳnh quang có dạng hình trụ được đặt khít vào một hộp giấy cứng dạng hình hộp chữ nhật (H.10.15). Hộp giấy có chiều dài bằng 0,6 m, đáy là hình vuông cạnh 4 cm. Tính diện tích xung quanh và thể tích của bóng đèn (giả sử bề dày của hộp giấy không đáng kể).
Đọc tiếp
Một bóng đèn huỳnh quang có dạng hình trụ được đặt khít vào một hộp giấy cứng dạng hình hộp chữ nhật (H.10.15). Hộp giấy có chiều dài bằng 0,6 m, đáy là hình vuông cạnh 4 cm. Tính diện tích xung quanh và thể tích của bóng đèn (giả sử bề dày của hộp giấy không đáng kể).
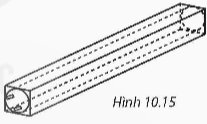
Thảo luận (1)Hướng dẫn giảiBóng đèn huỳnh quang đó có chiều cao bằng \(h = 0,6m = 60cm\) và đường kính đáy 4cm nên bán kính đáy là \(R = 2cm\).
Diện tích xung quanh của bóng đèn là:
\({S_{xq}} = 2\pi Rh = 2\pi .60.2 = 240\pi \left( {c{m^2}} \right)\).
Thể tích của bóng đèn là:
V = Sđáy.h\( = \pi {R^2}h\)\( = \pi {.2^2}.60 = 240\pi \left( {c{m^3}} \right)\).
(Trả lời bởi datcoder)
Bài tập 10.5 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 100)
Một dụng cụ gồm một phần có dạng hình trụ và một phần có dạng hình nón với các kích thước như Hình 10.16.
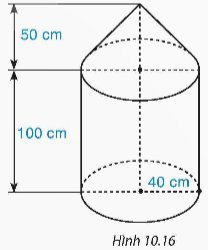
a) Tính thể tích của dụng cụ này.
b) Tính diện tích mặt ngoài của dụng cụ (không tính đáy của dụng cụ).
Thảo luận (1)Hướng dẫn giảiDụng cụ trên gồm:
+ Hình nón có chiều cao là 50cm, bán kính đáy bằng 40cm.
+ Hình trụ có chiều cao là 100cm, bán kính đáy bằng 40cm.
a) Thể tích của hình nón là:
\({V_1} = \frac{1}{3}\pi {.40^2}.50 = \frac{{80\;000\pi }}{3}\left( {c{m^3}} \right)\)
Thể tích của hình trụ là:
\({V_2} = \pi {.40^2}.100 = 160\;000\pi \left( {c{m^3}} \right)\)
Thể tích của dụng cụ là:
\(V = {V_1} + {V_2} = \frac{{80\;000\pi }}{3} + 160\;000\pi = \frac{{560\;000\pi }}{3}\left( {c{m^3}} \right)\)
b) Đường sinh của hình nón là:
\(\sqrt {{{50}^2} + {{40}^2}} = 10\sqrt {41} \left( {cm} \right)\).
Diện tích xung quanh của của hình nón là:
\({S_1} = \pi .10\sqrt {41} .40 = 400\sqrt {41} \pi \left( {c{m^2}} \right)\).
Diện tích xung quanh của của hình trụ là:
\({S_2} = 2\pi .40.100 = 8000\pi \left( {c{m^2}} \right)\).
Diện tích mặt ngoài của dụng cụ là:
\(S = {S_1} + {S_2} = 400\sqrt {41} \pi + 8000\pi = 400\pi \left( {\sqrt {41} + 20} \right)\left( {c{m^2}} \right)\)
(Trả lời bởi datcoder)
Bài tập 10.6 (SGK Kết nối tri thức với cuộc sống - Tập 2 - Trang 100)
Tính thể tích của hình tạo thành khi cho hình ABCD quay quanh AD một vòng (H.10.17).
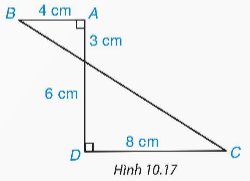
Thảo luận (1)Hướng dẫn giảiKhi quay hình ABCD quanh cạnh AD một vòng thì ta được một hình gồm hai hình nón có:
+ Hình nón thứ nhất có chiều cao bằng 3cm, bán kính đáy bằng 4cm.
+ Hình nón thứ hai có chiều cao bằng 6cm, bán kính đáy bằng 8cm.
Thể tích hình nón thứ nhất là: \({V_1} = \frac{1}{3}\pi {.4^2}.3 = 16\pi \left( {c{m^3}} \right)\).
Thể tích hình nón thứ hai là: \({V_2} = \frac{1}{3}\pi {.8^2}.6 = 128\pi \left( {c{m^3}} \right)\).
Thể tích hình cần tìm là: \(V = {V_1} + {V_2} = 16\pi + 128\pi = 144\pi \left( {c{m^3}} \right)\).
(Trả lời bởi datcoder)