Kết quả 40 lần nhảy xa của hai vận động viên nam Dũng và Huy được lần lượt thống kê trong Bảng 11 và Bảng 12 (đơn vị: mét):
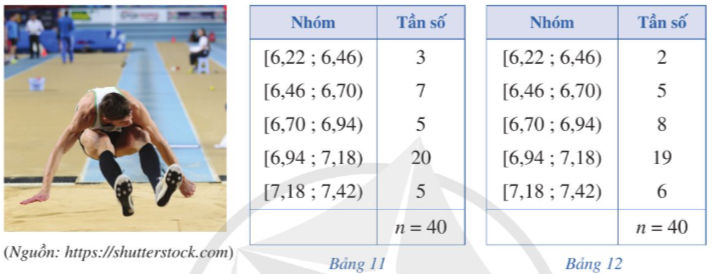
Kết quả nhảy xa của vận động viên nào đồng đều hơn?
Kết quả 40 lần nhảy xa của hai vận động viên nam Dũng và Huy được lần lượt thống kê trong Bảng 11 và Bảng 12 (đơn vị: mét):

Kết quả nhảy xa của vận động viên nào đồng đều hơn?
Xét mẫu số liệu ghép nhóm cho bởi Bảng 13.
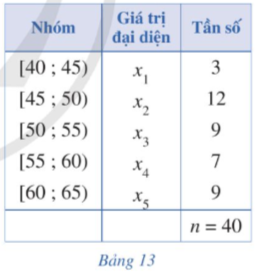
a) Tìm x1, x2, x3, x4, x5 lần lượt là giá trị đại diện của nhóm 1, nhóm 2, nhóm 3, nhóm 4, nhóm 5.
b) Tính số trung bình cộng \(\overline{x}\) của mẫu số liệu ghép nhóm đó.
c) Tính: \(s^2=\dfrac{3.\left(x_1-\overline{x}\right)^2+12.\left(x_2-\overline{x}\right)^2+9.\left(x_3-\overline{x}\right)^2+7.\left(x_4-\overline{x}\right)^2+9.\left(x_5-\overline{x}\right)^2}{40}\).
d) Tính \(s=\sqrt{s^2}\).
Thảo luận (1)Hướng dẫn giảia) \({x_1} = 42,5;{x_2} = 47,5;{x_3} = 52,5;{x_4} = 57,5;{x_5} = 62,5\).
b) \(\overline x = \frac{{3.42,5 + 12.47,5 + 9.52,5 + 7.57,5 + 9.62,5}}{{40}} = 53,375\).
c) \({s^2} = \frac{{3.{{({x_1} - \overline x )}^2} + 12{{({x_2} - \overline x )}^2} + 9{{({x_3} - \overline x )}^2} + 7{{({x_4} - \overline x )}^2} + 9{{({x_5} - \overline x )}^2}}}{{40}}\)
\( = \frac{{3.{{(42,5 - 53,375)}^2} + 12{{(47,5 - 53,375)}^2} + 9{{(52,5 - 53,375)}^2} + 7{{(57,5 - 53,375)}^2} + 9{{(62,5 - 53,375)}^2}}}{{40}}\)
\( = \frac{{2631}}{{64}}\).
d) \(s = \sqrt {{s^2}} = \sqrt {\frac{{2631}}{{64}}} \approx 6,41\).
(Trả lời bởi Nguyễn Quốc Đạt)
Tính phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm cho ở Bảng 17 (làm tròn kết quả đến hàng phần mười).
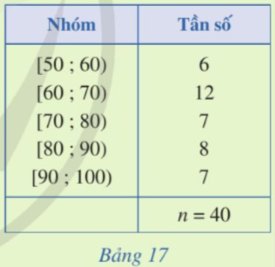
Thảo luận (1)Hướng dẫn giảiSố trung bình của mẫu số liệu là:
\(\overline x = \frac{{6.55 + 12.65 + 7.75 + 8.85 + 7.95}}{{40}} = \frac{{2980}}{{40}} = 74,5\).
Phương sai của mẫu số liệu là:
\({s^2} = \frac{1}{{40}}.[6.{(55 - 74,5)^2} + 12.{(65 - 74,5)^2} + 7.{(75 - 74,5)^2}\)
\( + 8.{(85 - 74,5)^2} + 7.{(95 - 74,5)^2}] = \frac{{7190}}{{40}} \approx 179,8\).
Độ lệch chuẩn của mẫu số liệu là:
\(\sqrt {{s^2}} = \sqrt {\frac{{7190}}{{40}}} \approx 13,4\).
(Trả lời bởi Nguyễn Quốc Đạt)
Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong một ngày. Số liệu được ghi lại trong Bảng 18.
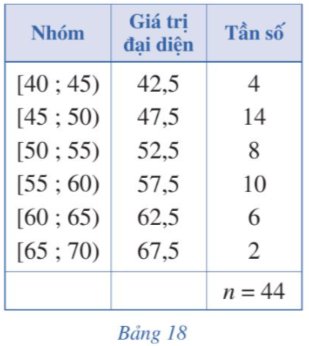
a) Phương sai của mẫu số liệu ghép nhóm trên là:
A. 53,2. B. 46,1. C. 30. D. 11.
b) Độ lệch chuẩn của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần mười) là:
A. 6,8. B. 7,3. C. 3,3. D. 46,1.
Thảo luận (1)Hướng dẫn giảia) Số trung bình cộng của mẫu số liệu ghép nhóm là: \(\overline x = \frac{{4.42,5 + 14.47,5 + 8.52,5 + 10.57,5 + 6.62,5 + 2.67,5}}{{44}} = \frac{{585}}{{11}}\)
Phương sai của mẫu số liệu ghép nhóm là:
\({s^2} = \frac{{4{{(42,5 - \frac{{585}}{{11}})}^2} + 14{{(47,5 - \frac{{585}}{{11}})}^2} + 8{{(52,5 - \frac{{585}}{{11}})}^2} + 10{{(57,5 - \frac{{585}}{{11}})}^2} + 6{{(62,5 - \frac{{585}}{{11}})}^2} + 2.{{(67,5 - \frac{{585}}{{11}})}^2}}}{{44}} \approx 46,12\)
Chọn B
b) Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(s = \sqrt {{s^2}} = \sqrt {46,12} \approx 6,8\)
Chọn A
(Trả lời bởi Nguyễn Quốc Đạt)
Bảng 19, Bảng 20 lần lượt biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của hai công ty A, B (đơn vị: triệu đồng).
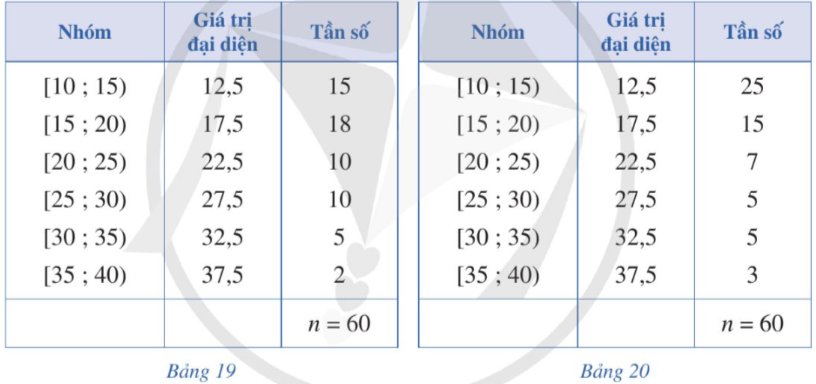
a) Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm lần lượt biểu diễn mức lương của hai công ty A, B.
b) Công ty nào có mức lương đồng đều hơn?
Thảo luận (1)Hướng dẫn giảiSố trung bình cộng của mẫu số liệu ghép nhóm của công ty A là: \(\overline {{x_A}} = \frac{{15.12,5 + 18.17,5 + 10.22,5 + 10.27,5 + 5.32,5 + 2.37,5}}{{60}} = \frac{{62}}{3}\)
Phương sai của mẫu số liệu ghép nhóm của công ty A là:
\({s_A}^2 = \frac{{15.{{(12,5 - \frac{{62}}{3})}^2} + 18.{{(17,5 - \frac{{62}}{3})}^2} + 10.{{(22,5 - \frac{{62}}{3})}^2} + 10.{{(27,5 - \frac{{62}}{3})}^2} + 5.{{(32,5 - \frac{{62}}{3})}^2} + 2.{{(37,5 - \frac{{62}}{3})}^2}}}{{60}} \approx 49,14\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm của công ty A là: \({s_A} = \sqrt {{s_A}^2} = \sqrt {49,13} \approx 7\)
Số trung bình cộng của mẫu số liệu ghép nhóm của công ty B là: \(\overline {{x_B}} = \frac{{25.12,5 + 15.17,5 + 7.22,5 + 5.27,5 + 5.32,5 + 3.37,5}}{{60}} = \frac{{229}}{{12}}\)
Phương sai của mẫu số liệu ghép nhóm của công ty B là:
\(\begin{array}{l}{s_B}^2 = \frac{{25.{{(12,5 - \frac{{229}}{{12}})}^2} + 15.{{(17,5 - \frac{{229}}{{12}})}^2} + 7.{{(22,5 - \frac{{229}}{{12}})}^2} + 5.{{(27,5 - \frac{{229}}{{12}})}^2} + 5.{{(32,5 - \frac{{229}}{{12}})}^2} + 3.{{(37,5 - \frac{{229}}{{12}})}^2}}}{{60}}\\ \approx 57,91\end{array}\)Độ lệch chuẩn của mẫu số liệu ghép nhóm của công ty B là: \({s_B} = \sqrt {{s_B}^2} = \sqrt {57,91} \approx 7,61\)
Nhận thấy độ lệch chuẩn của công ty A nhỏ hơn công ty B nên mức lương của công ty A đồng đều hơn
(Trả lời bởi Nguyễn Quốc Đạt)
Bảng 21 biểu diễn mẫu số liệu ghép nhóm về tuổi của cư dân trong một khu phố. Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
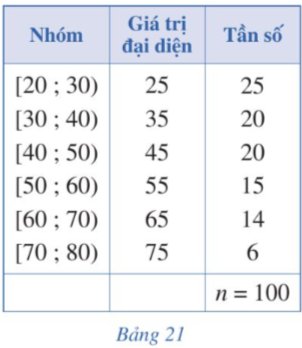
Thảo luận (1)Hướng dẫn giảiSố trung bình cộng của mẫu số liệu ghép nhóm là: \(\overline x = \frac{{25.25 + 20.35 + 20.45 + 15.55 + 14.65 + 6.75}}{{100}} = 44,1\)
Phương sai của mẫu số liệu ghép nhóm là:
\({s^2} = \frac{{25.{{(25 - 44,1)}^2} + 20.{{(35 - 44,1)}^2} + 20.{{(45 - 44,1)}^2} + 15.{{(55 - 44,1)}^2} + 14.{{(65 - 44,1)}^2} + 6.{{(75 - 44,1)}^2}}}{{100}} = 244,19\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(s = \sqrt {{s^2}} = \sqrt {244,19} \approx 15,63\)
(Trả lời bởi Nguyễn Quốc Đạt)