Tính 1 MeV/c2 ra đơn vị kilôgam.
Bài 2. Năng lượng liên kết hạt nhân
Câu hỏi 1 (SGK Cánh Diều - Trang 94)
Thảo luận (1)
Luyện tập 1 (SGK Cánh Diều - Trang 94)
Cho biết khối lượng của hạt nhân \(^{12}_6C\) là 11,99993 u. Sử dụng số liệu trong bảng 1.1 trang 92, tính độ hụt khối của hạt nhân \(^{12}_6C\).
Thảo luận (1)Hướng dẫn giảiĐộ chênh lệch giữa hai khối lượng đó được gọi là độ hụt khối của hạt nhân, kí hiệu là ∆m
độ hụt khối = tổng khối lượng các nucleon – khối lượng hạt nhân
\(\Delta m = Z.{m_p} + (A - Z).{m_n} - {m_X} = 6.1,00728 + (12 - 6).1,00866 - 11,99993 = 0,09571amu\)
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 4 (SGK Cánh Diều - Trang 95)
Hạt nhân \(^{56}_{26}Fe\) có năng lượng liên kết riêng bằng 8,8 MeV/nucleon là một trong những hạt nhân bền vững nhất trong tự nhiên. Tính độ hụt khối của hạt nhân này.
Thảo luận (1)Hướng dẫn giải\(\begin{array}{l}{W_{lk}} = 8,8A = 8,8.56 = 492,8MeV\\ \Rightarrow {W_{lk}} = \Delta m{c^2} = 492,8 \Rightarrow \Delta m = \frac{{{W_{lk}}}}{{{c^2}}} = 492,8MeV/{c^2}\end{array}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 2 (SGK Cánh Diều - Trang 94)
Tính năng lượng liên kết của hạt nhân \(^{12}_6C\) ra đơn vị MeV và đơn vị J.
Thảo luận (1)Hướng dẫn giảiNăng lượng liên kết của hạt nhân \({}_6^{12}C\) được tính theo công thức:
\(\begin{array}{l}{W_{lk}} = \Delta m.{c^2}\\ = \left( {Z.{m_p} + (A - Z).{m_n} - {m_X}} \right){c^2}\\ = \left( {6.1,00728 + (12 - 6).1,00866 - 11,99993} \right).{\left( {{{3.10}^8}} \right)^2}.1,{6605.10^{ - 27}}\\ = 1,{43.10^{ - 11}}J\end{array}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Câu hỏi mục 2 (SGK Cánh Diều - Trang 95)
Dựa vào Hình 2.3, sắp xếp các hạt nhân sau theo thứ tự độ bền vững tăng dần:
\(^6_3Li,^{12}_6C_7^{14}N,^{20}_{10}Ne\).
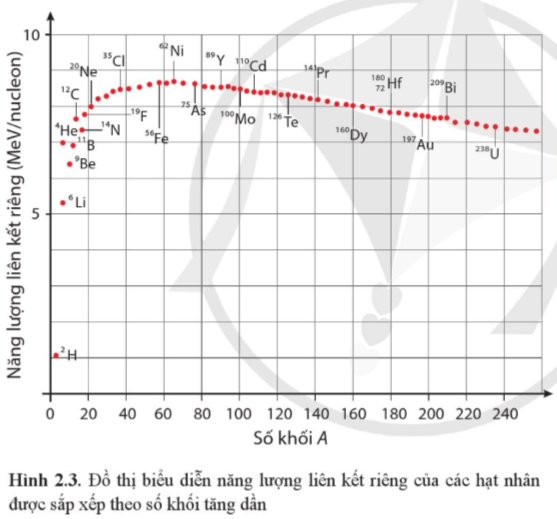
Thảo luận (1)Hướng dẫn giảiDựa vào hình 2.3 ta có thể sắp xếp được độ bền vững của các hạt nhân trên theo thứ tự tăng dần như sau: \({}_3^6Li,{}_7^{14}N,{}_6^{12}C,{}_{10}^{20}Ne\)
(Trả lời bởi Nguyễn Quốc Đạt)
Tìm hiểu thêm (SGK Cánh Diều - Trang 96)
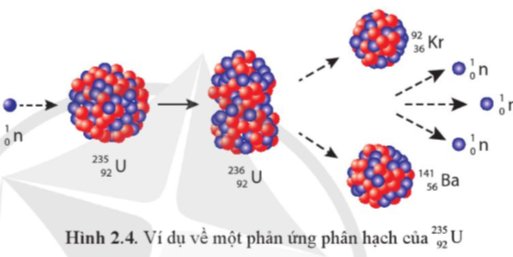
Ta có thể áp dụng hệ thức Einstein (2.2) để tính năng lượng tỏả ra của phản ứng phân hạch hạt nhân ^{235}_{92}U trong Hình 2.4. Trước phản ứng, tổng khối lượng các hạt làmtrước mn + mUSau phản ứng, tổng khối lượng các hạt làmsau mKr + mBa + 3mnThông qua phản ứng, khối lượng của hệ đã giảm đi một lượng là:mtrước - msauNhư vậy, phản ứng đã tỏả ra một năng lượng làEtỏa (mtrước - msau)c2Cho biết khối lượng nguyên tử của các hạt trong phản ứng phân hạch Hình 2.4 như trong bảng dưới đây:Tính năng l...
Đọc tiếp
Ta có thể áp dụng hệ thức Einstein (2.2) để tính năng lượng tỏả ra của phản ứng phân hạch hạt nhân \(^{235}_{92}U\) trong Hình 2.4. Trước phản ứng, tổng khối lượng các hạt là
mtrước = mn + mU
Sau phản ứng, tổng khối lượng các hạt là
msau = mKr + mBa + 3mn
Thông qua phản ứng, khối lượng của hệ đã giảm đi một lượng là:
mtrước - msau
Như vậy, phản ứng đã tỏả ra một năng lượng là
Etỏa = (mtrước - msau)c2
Cho biết khối lượng nguyên tử của các hạt trong phản ứng phân hạch Hình 2.4 như trong bảng dưới đây:
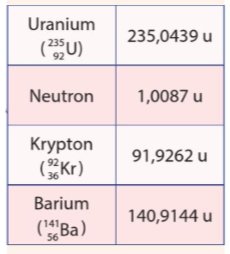
Tính năng lượng toả ra của phản ứng đó ra đơn vị MeV.
Thảo luận (1)Hướng dẫn giảiTrước phản ứng, tổng khối lượng các hạt là
mtrước = mn + mU = 1,0087 + 235,0439 = 236,0526 u
Sau phản ứng, tổng khối lượng các hạt là
msau = mKr + mBa + 3mn = 91,9262 + 140,9144 + 3.1,0087 = 235,8667 u
Như vậy, phản ứng đã tỏả ra một năng lượng là
Etỏa = (mtrước - msau)c2 = (236,0526 - 235,8667) c2 = 173,166 MeV
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 6 (SGK Cánh Diều - Trang 98)
Arktika là tàu phá băng chạy bằng năng lượng hạt nhân của Nga. Với chiều dài 173 m, cao 15 m, tàu được trang bị hai lò phản ứng hạt nhân, mỗi lò có công suất 175 MW, giúp tàu phá lớp băng dày đến 3 m.Nếu lò phản ứng này sử dụng năng lượng từ sự phân hạch của ^{235}_{92}U, mỗi phân hạch sinh ra trung bình 203 MeV; tính khối lượng ^{235}_{92}U mà lò phản ứng tiêu thụ trong 1 ngày. Cho số Avogadro NA 6,02.1023 nguyên tử/mol và khối lượng mol nguyên tử của ^{235}_{92}U là 235 g/mol.
Đọc tiếp
Arktika là tàu phá băng chạy bằng năng lượng hạt nhân của Nga. Với chiều dài 173 m, cao 15 m, tàu được trang bị hai lò phản ứng hạt nhân, mỗi lò có công suất 175 MW, giúp tàu phá lớp băng dày đến 3 m.
Nếu lò phản ứng này sử dụng năng lượng từ sự phân hạch của \(^{235}_{92}U\), mỗi phân hạch sinh ra trung bình 203 MeV; tính khối lượng \(^{235}_{92}U\) mà lò phản ứng tiêu thụ trong 1 ngày. Cho số Avogadro NA = 6,02.1023 nguyên tử/mol và khối lượng mol nguyên tử của \(^{235}_{92}U\) là 235 g/mol.

Thảo luận (1)Hướng dẫn giảiCông mà mỗi lò phản ứng hạt nhân của tàu đó tạo ra trong một ngày:
\(N = \frac{{1,{{512.10}^{13}}}}{{3,{{25206.10}^{ - 11}}}} = 4,{65.10^{23}}\) hạt
\(n = \frac{N}{{{N_A}}} = \frac{{4,{{65.10}^{23}}.2}}{{6,{{02.10}^{23}}}} = 1,545mol\)
Do đó khối lượng \({}_{92}^{235}U\) cần thiết cho cả 2 lò để tàu hoạt động trong một ngày là: \(m = n.M = 1,545.235 = 363,075g\)
(Trả lời bởi Nguyễn Quốc Đạt)
Vận dụng (SGK Cánh Diều - Trang 100)
Tìm tài liệu như hình ảnh, bài báo,… và dựa vào các tài liệu đó thảo luận với bạn bè về vai trò của một số ngành công nghiệp hạt nhân trong khoa học và đời sống
Thảo luận (1)Hướng dẫn giảiNgày nay, công nghệ hạt nhân không chỉ là một phần quan trọng của ngành công nghiệp, mà còn đóng vai trò không thể phủ nhận trong việc cải thiện đời sống và tiến bộ khoa học. Dưới đây là những ứng dụng và vai trò của ngành công nghiệp hạt nhân trong cuộc sống hàng ngày và trong lĩnh vực khoa học:
Y tế: Chẩn đoán và điều trị ung thư
Năng lượng:
+ Phát điện hạt nhân.
+ Nghiên cứu và phát triển năng lượng hạt nhân mới.
Khoa học:
+ Nghiên cứu vật lý hạt nhân.
+ Ứng dụng trong nghiên cứu vật lý khác.
Môi trường và bảo vệ:
+ Xử lý chất thải hạt nhân.
+ Giảm lượng khí thải carbon.
Những ứng dụng và vai trò của ngành công nghiệp hạt nhân đã và đang đóng một vai trò quan trọng trong việc cải thiện đời sống của con người, từ cung cấp năng lượng sạch đến cải thiện phương pháp chẩn đoán và điều trị bệnh tật. Tuy nhiên, cần phải chú ý đến các vấn đề liên quan đến an toàn, bảo vệ môi trường và quản lý chất thải hạt nhân để đảm bảo rằng các ứng dụng này được sử dụng một cách an toàn và bền vững.
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 5 (SGK Cánh Diều - Trang 96)
Năng lượng tỏả ra khi 1,000 kg ^{235}_{92}U bị phân hạch hoàn toàn theo phản ứng trong Hình 2.4 tương đương với năng lượng toả ra khi đốt cháy bao nhiêu tấn than đá?Cho biết: khối lượng mol nguyên tử của uranium là 235 g/mol; số Avogadro NA 6,02.1023 nguyên tử/mol.Mỗi kg than đá khi đốt cháy hoàn toàn toả ra 27.106 J năng lượng nhiệt.
Đọc tiếp
Năng lượng tỏả ra khi 1,000 kg \(^{235}_{92}U\) bị phân hạch hoàn toàn theo phản ứng trong Hình 2.4 tương đương với năng lượng toả ra khi đốt cháy bao nhiêu tấn than đá?
Cho biết: khối lượng mol nguyên tử của uranium là 235 g/mol; số Avogadro NA = 6,02.1023 nguyên tử/mol.
Mỗi kg than đá khi đốt cháy hoàn toàn toả ra 27.106 J năng lượng nhiệt.
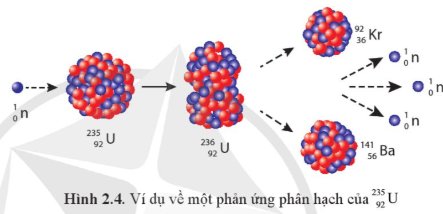
Thảo luận (1)Hướng dẫn giảiPhản ứng phân hạch của hạt nhân \({}_{92}^{235}U\) như trong Hình 2.4 tỏa ra năng lượng xấp xỉ bằng 173 MeV. Năng lượng này được gọi là năng lượng phân hạch, do đó để tính năng lượng tỏa ra khi 1000kg \({}_{92}^{235}U\) bị phân hạch hoàn toàn ta cần biết có bao nhiêu hạt nhân \({}_{92}^{235}U\) đã bị phân hạch. Ta có:
\(n = \frac{m}{M} = \frac{{{{10}^6}}}{{235,0439}} = 4254,52mol\)
\(N = n.{N_A} = 4254,52.6,{02.10^{23}} = 2,{56.10^{27}}\)hạt
\(A = 2,{56.10^{27}}.173.1,{602.10^{ - 13}} = 7,{1.10^{16}}J\)
Mà mỗi kg than đá khi đốt cháy hoàn toàn toả ra 27.106 J năng lượng nhiệt, số kg than đá cần thiết để sinh ra lượng nhiệt tương ứng như trên là:
\(\frac{{7,{{1.10}^{16}}}}{{{{27.10}^6}}} = 2,{6.10^9}kg\)
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 3 (SGK Cánh Diều - Trang 95)
Tính năng lượng liên kết riêng của hạt nhân \(^{12}_6C.\)
Thảo luận (1)Hướng dẫn giải\({W_{lkr}} = \frac{{{W_{lk}}}}{A} = \frac{{0,9571.931,5}}{{12}} = 7,4295MeV/nucleon\)
(Trả lời bởi Nguyễn Quốc Đạt)