Dùng MTCT, tìm các góc α (làm tròn đến phút), biết:
a) sinα = 0,3782;
b) cosα = 0,6251;
c) tanα = 2,154;
d) cotα = 3,253.
Dùng MTCT, tìm các góc α (làm tròn đến phút), biết:
a) sinα = 0,3782;
b) cosα = 0,6251;
c) tanα = 2,154;
d) cotα = 3,253.
Trở lại bài toán ở tình huống mở đầu. Trong một tòa chung cư, biết đoạn dốc vào sảnh tòa nhà dài 4 m, độ cao của đỉnh dốc bằng 0,4 m.
a) Hãy tính góc dốc.
b) Hỏi góc đó có đúng tiêu chuẩn của dốc cho người đi xe lăn không?
Thảo luận (1)Hướng dẫn giảia) Ta có: \(\sin \alpha = \frac{h}{a} = \frac{{0,4}}{4} = 0,1\), do đó \(\alpha \approx {5^0}44'.\)
b) \(\alpha \approx {5^0}44' < 6^0\)
Vậy góc đó đúng tiêu chuẩn cho người đi xe lăn.
(Trả lời bởi Nguyễn Quốc Đạt)
Để tính khoảng cách giữa hai địa điểm A, B không đo trực tiếp được, chẳng hạn A và B là hai địa điểm ở hai bên sông, người ta lấy điểm C về phía bờ sông có chứa B sao cho tam giác ABC vuông tại B. Ở bên bờ sông chứa B, người ta đo được \(\widehat{ACB}=\alpha\) và BC = a (H.4.10). Với các dữ liệu đó, đã tính được khoảng cách AB chưa? Nếu được, hãy tính AB, biết α = 55°, a = 70 m.
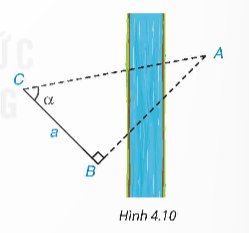
Thảo luận (1)Hướng dẫn giảiTa có: \(\tan \alpha = \frac{{AB}}{{BC}}\) hay \(\tan {55^0} = \frac{{AB}}{{70}}\) suy ra \(AB = 70.\tan {55^0} \approx 99,97\) m.
Vậy khoảng cách AB khoảng 99,97 m.
(Trả lời bởi Nguyễn Quốc Đạt)
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, coossin, tang, cotang của các góc nhọn B và C khi biết:
a) AB = 8 cm, BC = 17 cm;
b) AC = 0,9 cm, AB = 1,2 cm.
Thảo luận (1)Hướng dẫn giải
a)
Tam giác ABC vuông tại A nên ta có: \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)
Thay số ta có \({17^2} = {8^2} + A{C^2}\) hay \(A{C^2} = {17^2} - {8^2} = 225\) suy ra \(AC = 15\) cm (vì \(AC > 0\))
Ta có: \(\sin \widehat B = \cos \widehat C = \frac{{AC}}{{BC}} = \frac{{15}}{{17}}\)
\(\cos \widehat B = \sin \widehat C = \frac{{AB}}{{BC}} = \frac{8}{{17}}\)
\(\tan \widehat B = \cot \widehat C = \frac{{AC}}{{AB}} = \frac{{15}}{8}\)
\(\cot \widehat B = \tan \widehat C = \frac{{AB}}{{AC}} = \frac{8}{{15}}\)
b)
Tam giác ABC vuông tại A nên ta có: \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)
Thay số ta có \(B{C^2} = 1,{2^2} + 0,{9^2} = 2,25\) hay \(CB = \sqrt {2,25} = 1,5\) cm (vì \(BC > 0\))
Ta có: \(\sin \widehat B = \cos \widehat C = \frac{{AC}}{{BC}} = \frac{{0,9}}{{1,5}} = \frac{3}{5}\)
\(\cos \widehat B = \sin \widehat C = \frac{{AB}}{{BC}} = \frac{{1,2}}{{1,5}} = \frac{4}{5}\)
\(\tan \widehat B = \cot \widehat C = \frac{{AC}}{{AB}} = \frac{{0,9}}{{1,2}} = \frac{3}{4}\)
\(\cot \widehat B = \tan \widehat C = \frac{{AB}}{{AC}} = \frac{{1,2}}{{0,9}} = \frac{4}{3}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho tam giác vuông có một góc nhọn 60° và cạnh kề với góc 60° bằng 3 cm. Hãy tính cạnh đối của góc này.
Thảo luận (1)Hướng dẫn giải
Xét tam giác ABC vuông tại A ta có: \(\tan \widehat C = \frac{{AB}}{{AC}}\) hay \(\tan {60^0} = \frac{{AB}}{3}\) suy ra \(AB = 3.\tan {60^0} = 3\sqrt 3 \) cm.
Vậy cạnh đối của góc là \(3\sqrt 3 \) cm.
(Trả lời bởi Nguyễn Quốc Đạt)
Cho tam giác vuông có một góc nhọn bằng 30° và cạnh đối với góc này bằng 5 cm. Tính độ dài cạnh huyền của tam giác.
Thảo luận (1)Hướng dẫn giải
Xét tam giác ABC vuông tại A và có \(\widehat B = {30^0}\) nên ta có: \(\sin \widehat B = \frac{{AC}}{{BC}}\) hay \(\sin {30^0} = \frac{5}{{BC}}\) suy ra \(BC = \frac{5}{{\sin {{30}^0}}} = 10\) cm.
Vậy cạnh huyền của tam giác là 10 cm.
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và \(\sqrt{3}\). Tính góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật (sử dụng bảng giá trị lượng giác trang 69).
Thảo luận (1)Hướng dẫn giải
Xét hình chữ nhật EFHG có \(EG = FH = 3;EF = GH = \sqrt 3 \)
Góc giữa đường chéo và cạnh ngắn hơn là góc FEH
Ta có: \(\tan \widehat {FEH} = \frac{{FH}}{{EF}} = \frac{3}{{\sqrt 3 }} = \sqrt 3 \) nên \(\widehat {FEH} = {60^0}\)
Vậy góc giữa đường chéo và cạnh ngắn hơn là \({60^0}.\)
(Trả lời bởi Nguyễn Quốc Đạt)
a) Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45°:
sin55°, cos62°, tan57°, cot64°.
b) Tính \(\dfrac{\tan25^o}{\cot65^o}\); tan 34o - cot 56o.
Thảo luận (1)Hướng dẫn giảia) \(\sin {55^0} = \cos {35^0}; \)
\(\cos {62^0} = \sin {28^0}; \)
\(\tan {57^0} = \cot {33^0}; \)
\(\cot {64^0} = \tan {26^0}\)
b) \(\frac{{\tan {{25}^0}}}{{\cot {{65}^0}}} = \frac{{\tan {{25}^0}}}{{\tan {{25}^0}}} = 1\)
\(\tan {34^0} - \cot {56^0} = \tan {34^0} - \tan {34^0} = 0.\)
(Trả lời bởi Nguyễn Quốc Đạt)
Dùng MTCT, tính (làm tròn đến chữ số thập phân thứ ba):
a) sin40°12’;
b) cos52°54’;
c) tan63°36’;
d) cot35°20’.
Thảo luận (1)Hướng dẫn giảia) \(\sin {40^0}12' \approx 0,645\)
b) \(\cos {52^0}54' \approx 0,603\)
c) \(\tan {63^0}36' \approx 2,014\)
d) \(\cot {35^0}20' = \frac{1}{{\tan {{35}^0}20'}} \approx 1,411\)
(Trả lời bởi Nguyễn Quốc Đạt)
Dùng MTCT, tìm số đo của góc nhọn x (làm tròn đến phút), biết rằng:
a) sinx = 0,2368;
b) cosx = 0,6224;
c) tanx = 1,236;
d) cotx = 2,154.
Thảo luận (1)Hướng dẫn giảia) \(\sin x = 0,2368;\)
Ta có: \(\sin x = 0,2368\) nên \(x = {13^0}41'51,9'' \approx {13^0}42'\)
b) \(\cos x = 0,6224;\)
Ta có: \(\cos x = 0,6224\) nên \(x = {51^0}30'30,21'' \approx {51^0}31'\)
c) \(\tan x = 1,236;\)
Ta có: \(\tan x = 1,236\) nên \(x = {51^0}1'30,04'' \approx {51^0}2'\)
d) \(\cot x = 2,154.\)
Ta có: \(\cot x = 2,154\) nên \(x = {24^0}54'11,54'' \approx {24^0}54'\)
(Trả lời bởi Nguyễn Quốc Đạt)