Khi giữ nguyên áp suất của một khối lượng khí xác định thì thể tích của khí phụ thuộc như thế nào vào nhiệt độ của nó?
Bài 10. Định luật Charles
Mở đầu (SGK Kết nối tri thức với cuộc sống trang 41)
Thảo luận (1)
Hoạt động 1 (SGK Kết nối tri thức với cuộc sống trang 41)
Hãy giải thích cách vẽ đồ thị của hàm: V = V0 (1 + αt) trong Hình 10.1a.
Thảo luận (1)Hướng dẫn giải- Xác định hai điểm:
+ (0, V0): V0 là thể tích khí ở 0°C, được cho sẵn trong đề bài.
+ (t₁, V₁):
Chọn một giá trị t₁ bất kỳ.
Thay t₁ vào công thức V = V0 (1 + αt) để tính V₁.
Nối hai điểm bằng đường thẳng.
- Đường biểu diễn:
+ Đoạn thẳng đi qua hai điểm (0, V0) và (t₁, V₁)
+ Là đường thẳng đi lên vì thể tích khí tăng khi nhiệt độ tăng.
+ Độ dốc của đường thẳng phụ thuộc vào hệ số nở nhiệt α: α càng lớn, độ dốc càng lớn. α càng nhỏ, độ dốc càng nhỏ.
(Trả lời bởi Hà Quang Minh)
Hoạt động 2 (SGK Kết nối tri thức với cuộc sống trang 41)
Hãy chứng tỏ rằng nếu đối nhiệt độ Celcius t trong hệ thức (10.2) sang nhiệt độ Kelvin T tương ứng thì sẽ được một hệ thức mới chứng tỏ thể tích V của chất khí tỉ lệ thuận với nhiệt độ kevin: frac{V}{T} hằng số.
Đọc tiếp
Hãy chứng tỏ rằng nếu đối nhiệt độ Celcius t trong hệ thức (10.2) sang nhiệt độ Kelvin T tương ứng thì sẽ được một hệ thức mới chứng tỏ thể tích V của chất khí tỉ lệ thuận với nhiệt độ kevin: \(\frac{V}{T}\) = hằng số.
Thảo luận (1)Hướng dẫn giảiV = V₀(1 + αt) = V₀(1 + α(T - 273,15)) = V₀(1 + αT - 273,15α)
Ta có: V₀ và α là hằng số.
Khi T thay đổi, V cũng thay đổi theo.
Hệ số của T là 1 + α > 0.
Do đó, V tỉ lệ thuận với T.
(Trả lời bởi Hà Quang Minh)
Câu hỏi 1 (SGK Kết nối tri thức với cuộc sống trang 42)
Ứng với các áp suất khác nhau của cùng một lượng khí, ta có những đường đẳng áp khác nhau. Hình 10.2 vẽ hai đường đẳng áp của cùng một lượng khí ứng với hai áp suất p1 và p2. Hãy so sánh p1 và p2.
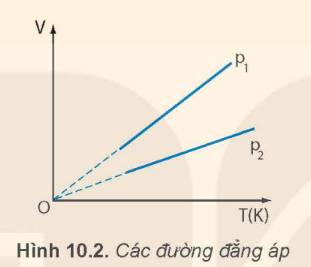
Thảo luận (1)Hướng dẫn giảip1 > p2
(Trả lời bởi Hà Quang Minh)
Câu hỏi 2 (SGK Kết nối tri thức với cuộc sống trang 42)
Hãy tìm ví dụ về ứng dụng định luật Charles trong đời sống.
Thảo luận (1)Hướng dẫn giải- Bơm xe đạp: Khi bơm xe đạp, ta nén khí trong bình chứa. Theo định luật Charles, khi thể tích khí giảm (do bị nén), áp suất khí tăng. Nhờ vậy, áp suất khí trong bình đủ lớn để đẩy lốp xe phồng lên.
- Nấu ăn: Khi nấu ăn, ta thường đun nóng thức ăn trong nồi. Khi nhiệt độ tăng, áp suất khí trong nồi cũng tăng theo. Do đó, nếu nồi kín, áp suất cao có thể khiến nắp nồi bật ra. Để tránh tình trạng này, người ta thường thiết kế nồi có van an toàn để thoát khí khi áp suất quá cao.
(Trả lời bởi Hà Quang Minh)
Hoạt động: Thí nghiệm và trả lời câu hỏi (SGK Kết nối tri thức với cuộc sống trang 43)
Chuẩn bị:- Xi lanh thủy tinh dung tích 50 mL, có độ chia nhỏ nhất 1 mL (1).- Nhiệt kế điện tử (2).- Ba cốc thủỷ tinh (3), (4), (5).- Nút cao su để bịt đầu ra của xi lanh.- Giá đỡ thí nghiệm (6).- Nước đá, nước ấm, nước nóng.- Dầu bôi trơn. Tiến hành:Bước 1: Cho một chút dầu bôi trơn vào pit-tông để pit-tông dễ dàng di chuyển trong xi lanh. Điều chỉnh pit-tông ở mức 30 mL, bịt đầu ra của xi lanh bằng nút cao su.Bước 2: Ghi giá trị nhiệt độ phòng và thể tích không khí trong xi lanh vào vở tương tự...
Đọc tiếp
Chuẩn bị:
- Xi lanh thủy tinh dung tích 50 mL, có độ chia nhỏ nhất 1 mL (1).
- Nhiệt kế điện tử (2).
- Ba cốc thủỷ tinh (3), (4), (5).
- Nút cao su để bịt đầu ra của xi lanh.
- Giá đỡ thí nghiệm (6).
- Nước đá, nước ấm, nước nóng.
- Dầu bôi trơn.

Tiến hành:
Bước 1: Cho một chút dầu bôi trơn vào pit-tông để pit-tông dễ dàng di chuyển trong xi lanh. Điều chỉnh pit-tông ở mức 30 mL, bịt đầu ra của xi lanh bằng nút cao su.
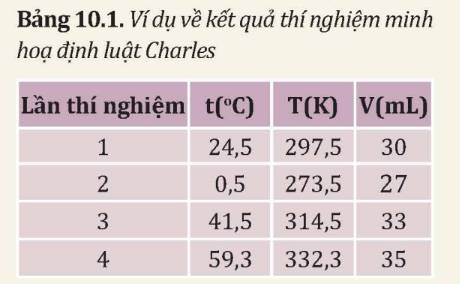
Bước 2: Ghi giá trị nhiệt độ phòng và thể tích không khí trong xi lanh vào vở tương tự như Bảng 10.1.
Bước 3: Đổ nước đá vào cốc (3).
Bước 4: Nhúng xi lanh và nhiệt kế vào cốc. Sau khoảng thời gian 3 phút, ghi giá trị thế tích V của không khí trong xi lanh và nhiệt độ t vào bảng số liệu.
Bước 5: Lần lượt đổ nước ấm vào cốc (4) và nước nóng vào cốc (5). Thực hiện tương tự bước 4 ở mỗi trường hợp.
Từ kết quả thí nghiệm, thực hiện các yêu cầu sau:
- Tính T, \(\frac{V}{T}\)
- Từ số liệu thu được, vẽ đồ thị mối quan hệ V, T.
Hoạt động 1 (SGK Kết nối tri thức với cuộc sống trang 43)
Kết quả thí nghiệm thu được có phù hợp với định luật Charles không?
Thảo luận (1)Hướng dẫn giảiKết quả thí nghiệm thu được phù hợp với định luật Charles.
(Trả lời bởi Hà Quang Minh)
Hoạt động 2 (SGK Kết nối tri thức với cuộc sống trang 43)
Giải thích tại sao có thể coi quá trình biến đổi trạng thải của khí trong thí nghiệm trên là quá trình đẳng áp?
Thảo luận (1)Hướng dẫn giảiDo áp suất khí trong thí nghiệm gần như không đổi nên ta có thể coi đây là quá trình đẳng áp.
(Trả lời bởi Hà Quang Minh)
Vận dụng 1 (SGK Kết nối tri thức với cuộc sống trang 44)
Thể tích của một lượng khí xác định tăng thêm 10% khi nhiệt độ của khí được tăng tới 47 °C. Xác định nhiệt độ ban đầu của lượng khí, biết quá trình trên là đẳng áp.
Thảo luận (1)Hướng dẫn giải\(\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}} \Rightarrow {T_1} = \frac{{{V_1}{T_2}}}{{{V_2}}} = \frac{{{V_1}.47}}{{1,1.{V_1}}} = 42,73^\circ C\)
(Trả lời bởi Hà Quang Minh)
Vận dụng 2 (SGK Kết nối tri thức với cuộc sống trang 44)
Một khối lượng khí 12 g có thể tích 4 lít ở nhiệt độ 7 °C. Sau khi được đun nóng đẳng áp thì khối lượng riêng của khí là 1,2 g/lít. Xác định nhiệt độ của khí sau khi được đun nóng.
Thảo luận (1)Hướng dẫn giải\(\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}} \Rightarrow {T_2} = \frac{{{V_2}{T_1}}}{{{V_1}}} = \frac{{\frac{4}{{1,2}}.7}}{4} = 8,89^\circ C\)
(Trả lời bởi Hà Quang Minh)