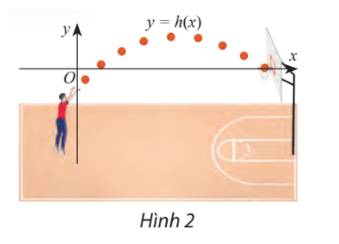
Độ cao (tính bằng mét) của một quả bóng so với vành rổ khi bóng di chuyển được x mét theo phương ngang được mô phỏng bằng hàm số \(h\left( x \right) = - 0,1{x^2} + x - 1\). Trong các khoảng nào của x thì bóng nằm: cao hơn vành rổ, thấp hơn vành rổ và ngang vành rổ? Làm tròn các kết quả đến hàng phần mười.