Với giá trị nào của x thì biểu thức \(A=\sqrt{3x+6}\) xác định? Tính giá trị của A khi x = 5 (kết quả làm tròn đến chữ số thập phân thứ hai)
Bài 1. Căn bậc hai
Thực hành 7 (SGK Chân trời sáng tạo - Tập 1 - Trang 40)
Thảo luận (1)
Thực hành 8 (SGK Chân trời sáng tạo - Tập 1 - Trang 40)
Cho biểu thức \(P=\sqrt{a^2-b^2}\). Tính giá trị của P khi:
a) a = 5, b = 0; b) a = 5, b = −5; c) a = 2, b = −4.
Thảo luận (1)Hướng dẫn giảia) Thay a = 5; b = 0 vào P = \(\sqrt {{a^2} - {b^2}} \), ta được:
P = \(\sqrt {{5^2} - {0^2}} = 5\)
b) Thay a = 5; b = -5 vào P = \(\sqrt {{a^2} - {b^2}} \), ta được:
P = \(\sqrt {{5^2} - {{( - 5)}^2}} = 0\)
c) Thay a = 2; b = -4 vào P = \(\sqrt {{a^2} - {b^2}} \) thì biểu thức P không khác định vì
a2 – b2 = -12 < 0 .
(Trả lời bởi datcoder)
Vận dụng 2 (SGK Chân trời sáng tạo - Tập 1 - Trang 40)
Một trạm phát sóng được đặt ở vị trí B cách đường tàu một khoảng AB 300 m. Đầu tàu đang ở vị trí C, cách vị trí A một khoảng AC x (m) (Hình 4).a) Viết biểu thức (theo x) biểu thị khoảng cách từ trạm phát sóng đến đầu tàu.b) Tính khoảng cách trên khi x 400, x 1 000 (kết quả làm tròn đến hàng đơn vị của mét).
Đọc tiếp
Một trạm phát sóng được đặt ở vị trí B cách đường tàu một khoảng AB = 300 m. Đầu tàu đang ở vị trí C, cách vị trí A một khoảng AC = x (m) (Hình 4).
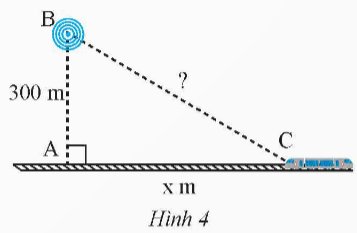
a) Viết biểu thức (theo x) biểu thị khoảng cách từ trạm phát sóng đến đầu tàu.
b) Tính khoảng cách trên khi x = 400, x = 1 000 (kết quả làm tròn đến hàng đơn vị của mét).
Thảo luận (1)Hướng dẫn giảia) Ta có khoảng cách từ trạm phát sóng đến đầu tàu là: \(\sqrt {{{300}^2} + {x^2}} \) (m)
b) Thay x = 400 thì khoảng cách từ trạm phát sóng đến đầu tàu là: \(\sqrt {{{300}^2} + {{400}^2}} = 500\) (m)
Thay x = 1000 thì khoảng cách từ trạm phát sóng đến đầu tàu là: \(\sqrt {{{300}^2} + {{1000}^2}} \approx 1044\) (m)
(Trả lời bởi datcoder)
Bài tập 1 (SGK Chân trời sáng tạo - Tập 1 - Trang 41)
Tìm các căn bậc hai của mỗi số sau:
a) 16; b) 2 500; c) \(\dfrac{4}{81}\); d) 0,09.
Thảo luận (1)Hướng dẫn giảia) Ta có 42 = 16, nên 16 có hai căn bậc hai là 4 và – 4
b) Ta có 502 = 2500, nên 2500 có hai căn bậc hai là 50 và – 50
c) Ta có \({\left( {\frac{2}{9}} \right)^2} = \frac{4}{{81}}\) nên \(\frac{4}{{81}}\) có hai căn bậc hai là \(\frac{2}{9}\) và – \(\frac{2}{9}\)
d) Ta có 0,32 = 0,09 nên 0,09 có hai căn bậc hai là 0,3 và – 0,3.
(Trả lời bởi datcoder)
Bài tập 2 (SGK Chân trời sáng tạo - Tập 1 - Trang 41)
Tính:
a) \(\sqrt{100}\); b) \(\sqrt{225}\); c) \(\sqrt{2,25}\); d) \(\sqrt{\dfrac{16}{225}}\).
Thảo luận (1)Hướng dẫn giải
Bài tập 3 (SGK Chân trời sáng tạo - Tập 1 - Trang 41)
Biết rằng 252 = 625, tìm các căn bậc hai của các số 625 và 0,0625.
Thảo luận (1)Hướng dẫn giải625 có hai căn bậc hai là 25 và – 25
0,0625 có hai căn bậc hai là 0,25 và – 0,25.
(Trả lời bởi datcoder)
Bài tập 4 (SGK Chân trời sáng tạo - Tập 1 - Trang 41)
Sử dụng máy tính cầm tay, tính (kết quả làm tròn đến chữ số thập phân thứ tư):
a) \(\sqrt{54}\); b) \(\sqrt{24,68}\); c) \(\sqrt{5}+\sqrt{6}+\sqrt{7}\).
Thảo luận (1)Hướng dẫn giảia) \(\sqrt {54} \approx 7,3485\)
b) \(\sqrt {24,68} \approx 4,9679\)
c) \(\sqrt 5 + \sqrt 6 + \sqrt 7 \approx 7,3313\)
(Trả lời bởi datcoder)
Bài tập 5 (SGK Chân trời sáng tạo - Tập 1 - Trang 41)
Tính giá trị của các biểu thức:
a) \(\left(\sqrt{5,25}\right)^2+\left(-\sqrt{1,75}\right)^2\); b) \(\left(\sqrt{102}\right)^2-\sqrt{98^2}\).
Thảo luận (1)Hướng dẫn giảia) \({\left( {\sqrt {5,25} } \right)^2} + {\left( { - \sqrt {1,75} } \right)^2} = 5,25 + 1,75 = 7\)
b) \({\left( {\sqrt {102} } \right)^2} - \sqrt {{{98}^2}} = 102 - 98 = 4\)
(Trả lời bởi datcoder)
Bài tập 6 (SGK Chân trời sáng tạo - Tập 1 - Trang 41)
Tìm x, biết:
a) x2 = 121; b) 4x2 = 9; c) x2 = 10.
Thảo luận (2)Hướng dẫn giải
Bài tập 7 (SGK Chân trời sáng tạo - Tập 1 - Trang 41)
Tính giá trị của các biểu thức sau khi x = 16, y = 9.
a) \(\sqrt{x}+\sqrt{y}\); b) \(\sqrt{x+y}\); c) \(\dfrac{1}{2}\sqrt{xy}\); d) \(\dfrac{1}{6}x\sqrt{y}\).
Thảo luận (1)Hướng dẫn giảia) Thay x = 16; y = 9, ta được \(\sqrt {16} + \sqrt 9 = 4 + 3 = 7\)
b) Thay x = 16; y = 9, ta được \(\sqrt {16 + 9} = \sqrt {25} = 5\)
c) Thay x = 16; y = 9, ta được \(\frac{1}{2}\sqrt {16.9} = 6\)
c) Thay x = 16; y = 9, ta được \(\frac{1}{6}.16\sqrt 9 = 8\)
(Trả lời bởi datcoder)