Bài 1. Các góc ở vị trí đặc biệt

Hướng dẫn giải

Vì hai góc \(\widehat {xOy},\widehat {yOz}\) kề bù với nhau nên

\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} = 180^\circ \\ \Rightarrow 25^\circ  + \widehat {yOz} = 180^\circ \\ \Rightarrow \widehat {yOz} = 180^\circ  - 25^\circ  = 155^\circ \end{array}\)

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

Vì \(\widehat {AOB}\) và \(\widehat {BOC}\) là 2 góc kề nhau nên \(\widehat {AOB} + \widehat {BOC} = \widehat {AOC}\), mà \(\widehat {AOC} = 80^\circ \) nên \(\widehat {AOB} + \widehat {BOC} = 80^\circ \)

Vì \(\widehat {AOB} = \frac{1}{5}.\widehat {AOC}\) nên \(\widehat {AOB} = \frac{1}{5}.80^\circ  = 16^\circ \)

Như vậy,

\(\begin{array}{l}16^\circ  + \widehat {BOC} = 80^\circ \\ \Rightarrow \widehat {BOC} = 80^\circ  - 16^\circ  = 64^\circ \end{array}\)

Vậy \(\widehat {AOB} = 16^\circ ;\widehat {BOC} = 64^\circ \)

(Trả lời bởi Hà Quang Minh)

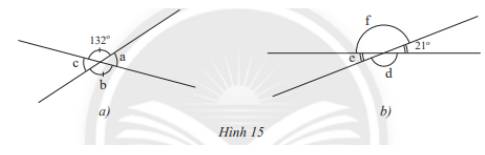
Hướng dẫn giải

a) Ta có: b = 132\(^\circ \)( 2 góc đối đỉnh)

a + 132\(^\circ \) =180\(^\circ \) (2 góc kề bù) nên a = 180\(^\circ \) - 132\(^\circ \) = 48\(^\circ \)

c = a = 48\(^\circ \)(2 góc đối đỉnh)

b) e = 21\(^\circ \)(2 góc đối đỉnh)

d + 21\(^\circ \) =180\(^\circ \) (2 góc kề bù) nên d = 180\(^\circ \)- 21\(^\circ \)= 159\(^\circ \)

f = d =159\(^\circ \)(2 góc đối đỉnh)

(Trả lời bởi Hà Quang Minh)

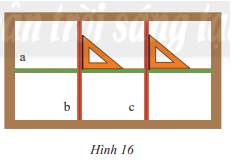
Hướng dẫn giải

Ta thấy: a \( \bot \)b và a \( \bot \)c

(Trả lời bởi Hà Quang Minh)