Cho tam giác ABC. Hai đường trung tuyến AM và BN cắt nhau tại G.
Tìm các số a, b biết: \(\overrightarrow {AG} = a.\overrightarrow {AM} ;\overrightarrow {GN} = b.\overrightarrow {GB} \)
Cho tam giác ABC. Hai đường trung tuyến AM và BN cắt nhau tại G.
Tìm các số a, b biết: \(\overrightarrow {AG} = a.\overrightarrow {AM} ;\overrightarrow {GN} = b.\overrightarrow {GB} \)
Cho ba điểm A, B, C. Chứng minh \(3\left( {\overrightarrow {AB} + 2\overrightarrow {BC} } \right) - 2\left( {\overrightarrow {AB} + 3\overrightarrow {BC} } \right) = \overrightarrow {AB} \)
Thảo luận (1)Hướng dẫn giảiTa có: \(3\left( {\overrightarrow {AB} + 2\overrightarrow {BC} } \right) - 2\left( {\overrightarrow {AB} + 3\overrightarrow {BC} } \right)\)\( = 3\overrightarrow {AB} + 3.\left( {2\overrightarrow {BC} } \right) - \left[ {2\overrightarrow {AB} + 2.\left( {3\overrightarrow {BC} } \right)} \right]\)
\[ = 3\overrightarrow {AB} + 6.\overrightarrow {BC} - \left( {2\overrightarrow {AB} + 6.\overrightarrow {BC} } \right)\]\[ = 3\overrightarrow {AB} + 6.\overrightarrow {BC} - 2\overrightarrow {AB} - 6.\overrightarrow {BC} \]
\[ = \left( {3\overrightarrow {AB} - 2\overrightarrow {AB} } \right) + \left( {6.\overrightarrow {BC} - 6.\overrightarrow {BC} } \right) = \overrightarrow {AB} .\]
(Trả lời bởi Hà Quang Minh)
Cho tam giác ABC có G là trọng tâm. Chứng minh \(\overrightarrow {AB} + \overrightarrow {AC} = 3\overrightarrow {AG} .\)
Thảo luận (1)Hướng dẫn giảiVới điểm M bất kì ta có: \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
Chọn M trùng A, ta được: \(\overrightarrow {AA} + \overrightarrow {AB} + \overrightarrow {AC} = 3\overrightarrow {AG} \Leftrightarrow \overrightarrow {AB} + \overrightarrow {AC} = 3\overrightarrow {AG} .\)
(Trả lời bởi Hà Quang Minh)
Cho ba điểm phân biệt A, B, C.
a) Nếu ba điểm A, B, C thẳng hàng thì hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương hay không?
b) Ngược lại, nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì ba điểm A, B, C có thẳng hàng hay không?
Thảo luận (1)Hướng dẫn giảia) Nếu A, B, C thẳng hàng thì đường thẳng AB trùng đường thẳng AC, do đó hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương.
b) Nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì đường thẳng AB trùng đường thẳng AC, do đó ba điểm A, B, C có thẳng hàng.
(Trả lời bởi Hà Quang Minh)
Ở hình 61, tìm k trong mỗi trường hợp sau:
a) \(\overrightarrow {AC} = k.\overrightarrow {AD} \)
b) \(\overrightarrow {BD} = k.\overrightarrow {DC} \)
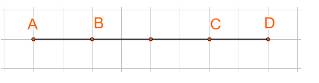
Thảo luận (1)Hướng dẫn giảia) Ta có: \(\overrightarrow {AC} ,\overrightarrow {AD} \)là hai vecto cùng hướng và \(\left| {\overrightarrow {AC} } \right| = \frac{3}{4}\left| {\overrightarrow {AD} } \right|\)
Suy ra \(\overrightarrow {AC} = \frac{3}{4}\overrightarrow {AD} .\) Vậy \(k = \frac{3}{4}.\)
b) Ta có: \(\overrightarrow {BD} ,\overrightarrow {DC} \)là hai vecto ngược hướng và \(\left| {\overrightarrow {BD} } \right| = 3\left| {\overrightarrow {DC} } \right|\)
Suy ra \(\overrightarrow {BD} = - 3\overrightarrow {DC} .\) Vậy \(k = - 3.\)
(Trả lời bởi Hà Quang Minh)
Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào sau đây là đúng?
A. \(\overrightarrow {MN} = 2\overrightarrow {PQ} \)
B. \(\overrightarrow {MN} = 2\overrightarrow {NP} \)
C. \(\overrightarrow {MN} = - 2\overrightarrow {PQ} \)
D. \(\overrightarrow {MQ} = - 2\overrightarrow {NP} \)
Thảo luận (1)Hướng dẫn giải
Do MQ và PN không song song với nhau nên \(\overrightarrow {MQ} \ne k\overrightarrow {NP} \). Vậy loại B và D.
Ta có: \(\overrightarrow {MN} ,\overrightarrow {PQ} \)là hai vecto ngược hướng và \(\left| {\overrightarrow {MN} } \right| = 2\left| {\overrightarrow {PQ} } \right|\)
Suy ra \(\overrightarrow {MN} = - 2\overrightarrow {PQ} \)
Vậy chọn C.
(Trả lời bởi Hà Quang Minh)
Cho đoạn thẳng AB = 6 cm.
a) Xác định điểm C thỏa mãn \(\overrightarrow {AC} = \frac{1}{2}\overrightarrow {AB} \)
b) Xác định điểm D thỏa mãn \(\overrightarrow {AD} = - \frac{1}{2}\overrightarrow {AB} \)
Thảo luận (1)Hướng dẫn giảia) Ta có: \(\overrightarrow {AC} = \frac{1}{2}\overrightarrow {AB} \)
\( \Rightarrow \)Hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng hướng và \(AC = \frac{1}{2}AB\).
Vậy C là trung điểm của AB.
b) Ta có: \(\overrightarrow {AD} = - \frac{1}{2}\overrightarrow {AB} = - \overrightarrow {AC} \)
\( \Rightarrow \)Hai vecto \(\overrightarrow {AD} ,\overrightarrow {AC} \) ngược hướng và \(AD = AC\).
Vậy A là trung điểm DC.
(Trả lời bởi Hà Quang Minh)
Cho tam giác ABC có M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh:
a) \(\overrightarrow {AP} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AN} \)
b) \(\overrightarrow {BC} + 2\overrightarrow {MP} = \overrightarrow {BA} \)
Thảo luận (1)Hướng dẫn giải
a) Ta có: \(\overrightarrow {BC} ,\overrightarrow {PN} \) là hai vecto cùng hướng và \(\frac{1}{2}\left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {PN} } \right|\)
\( \Rightarrow \frac{1}{2}\overrightarrow {BC} = \overrightarrow {PN} \)\( \Rightarrow \overrightarrow {AP} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AP} + \overrightarrow {PN} = \overrightarrow {AN} \)
b) Ta có: \(\overrightarrow {MP} ,\overrightarrow {CA} \) là hai vecto cùng hướng và \(2\left| {\overrightarrow {MP} } \right| = \left| {\overrightarrow {CA} } \right|\)
\( \Rightarrow 2\overrightarrow {MP} = \overrightarrow {CA} \)\( \Rightarrow \overrightarrow {BC} + 2\overrightarrow {MP} = \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow {BA} \)
(Trả lời bởi Hà Quang Minh)
Cho tam giác ABC. Các điểm D, E thuộc cạnh BC thỏa mãn BD = DE = EC (Hình 62). Giả sử \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AC} = \overrightarrow b .\) Biểu diễn các vecto \(\overrightarrow {BC} ,\overrightarrow {BD} ,\overrightarrow {BE} ,\overrightarrow {AD} ,\overrightarrow {AE} \) theo \(\overrightarrow a ,\overrightarrow b .\)
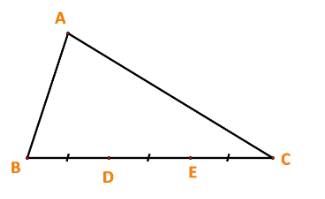
Thảo luận (1)Hướng dẫn giải
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \Leftrightarrow \overrightarrow {BC} = \overrightarrow b - \overrightarrow a \)
Lại có: vecto \(\overrightarrow {BD} ,\overrightarrow {BC} \) cùng hướng và \(\left| {\overrightarrow {BD} } \right| = \frac{1}{3}\left| {\overrightarrow {BC} } \right|\)
\( \Rightarrow \overrightarrow {BD} = \frac{1}{3}\overrightarrow {BC} = \frac{1}{3}(\overrightarrow b - \overrightarrow a )\)
Tương tự: vecto \(\overrightarrow {BE} ,\overrightarrow {BC} \) cùng hướng và \(\left| {\overrightarrow {BE} } \right| = \frac{2}{3}\left| {\overrightarrow {BC} } \right|\)
\( \Rightarrow \overrightarrow {BE} = \frac{2}{3}\overrightarrow {BC} = \frac{2}{3}(\overrightarrow b - \overrightarrow a )\)
Ta có:
\(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \Leftrightarrow \overrightarrow {AD} = \overrightarrow a + \frac{1}{3}(\overrightarrow b - \overrightarrow a ) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b \)
\(\overrightarrow {AB} + \overrightarrow {BE} = \overrightarrow {AE} \Leftrightarrow \overrightarrow {AE} = \overrightarrow a + \frac{2}{3}(\overrightarrow b - \overrightarrow a ) = \frac{1}{3}\overrightarrow a + \frac{2}{3}\overrightarrow b \)
(Trả lời bởi Hà Quang Minh)
Cho tứ giác ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD. Gọi G là trung điểm của đoạn thẳng MN, E là trọng tâm tam giác BCD. Chứng minh:
a) \(\overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = 4\overrightarrow {EG} \)
b) \(\overrightarrow {EA} = 4\overrightarrow {EG} \)
c) Điểm G thuộc đoạn thẳng AE và \(\overrightarrow {AG} = \frac{3}{4}\overrightarrow {AE} \)
Thảo luận (1)Hướng dẫn giảia) Ta có: \(\overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} \)\( = 4\overrightarrow {EG} + \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} \)
Mà: \(\overrightarrow {GA} + \overrightarrow {GB} = 2\overrightarrow {GM} ;\) (do M là trung điểm của AB)
\(\overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {GN} \) (do N là trung điểm của CD)
\( \Rightarrow \overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = 4\overrightarrow {EG} + 2(\overrightarrow {GM} + \overrightarrow {GN} ) = 4\overrightarrow {EG} \) (do G là trung điểm của MN)
b) Vì E là trọng tâm tam giác BCD nên \(\overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = \overrightarrow 0 \)
Từ ý a ta suy ra \(\overrightarrow {EA} = 4\overrightarrow {EG} \)
c) Ta có: \(\overrightarrow {EA} = 4\overrightarrow {EG} \Leftrightarrow \overrightarrow {EA} = 4.(\overrightarrow {EA} + \overrightarrow {AG} ) \Leftrightarrow - 3\overrightarrow {EA} = 4\overrightarrow {AG} \)
\( \Leftrightarrow 3\overrightarrow {AE} = 4\overrightarrow {AG} \) hay \(\overrightarrow {AG} = \frac{3}{4}\overrightarrow {AE} \)
Suy ra A, G, E thẳng hàng và \(AG = \frac{3}{4}AE \) nên G thuộc đoạn AE.
(Trả lời bởi Hà Quang Minh)