Question

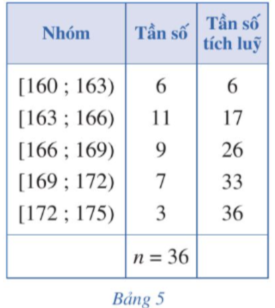
Xét mẫu số liệu ghép nhóm cho bởi Bảng 5.

a)

- Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\dfrac{n}{4}=\dfrac{36}{4}=9\) có đúng không?

- Tìm đầu mút trái s, độ dài h, tần số n₂ của nhóm 2; tần số tích lũy cf₁ của nhóm 1. Sau đó, hãy tính tứ phân vị thứ nhất Q₁­ của mẫu số liệu đã cho theo công thức sau:

\(Q_1=s+\left(\dfrac{9-cf_1}{a_2}\right).h\).

b)

- Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\dfrac{n}{2}=\dfrac{36}{2}=18\) có đúng không?

- Tìm đầu mút trái r, độ dài d, tần số n₃ của nhóm 3; tần số tích lũy cf₂ của nhóm 2. Sau đó, hãy tính tứ phân vị thứ hai Q₂ của mẫu số liệu đã cho theo công thức sau:

\(Q_2=r+\left(\dfrac{18-cf_2}{n_3}\right).d\).

c)

- Nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\dfrac{3n}{4}=\dfrac{3.36}{4}=27\) có đúng không?

- Tìm đầu mút trái t, độ dài l, tần số n4 của nhóm 4; tần số tích lũy cf₃ của nhóm 3. Sau đó, hãy tính tứ phân vị thứ hai Q₃ của mẫu số liệu đã cho theo công thức sau:

\(Q_3=t+\left(\dfrac{27-cf_3}{n_4}\right).l\).

d) Tìm hiệu Q₃ – Q₁.