Question

Xét hình phẳng giới hạn bởi đường thẳng y = f(x) = x + 1, trục hoành và hai đường thẳng x = −2; x = 1 (H.4.12).

a) Tính diện tích S của hình phẳng này.

b) Tính \(\int\limits^1_{-2}\left|f\left(x\right)\right|dx\) và so sánh với S.

Answer 1

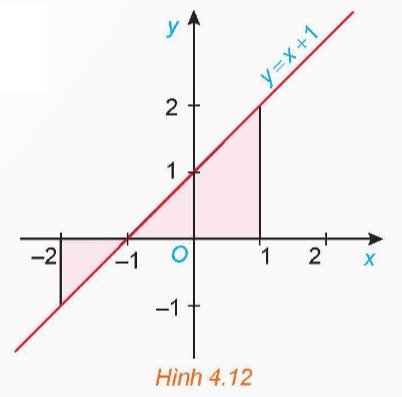
a) Đặt tên các điểm như hình vẽ. Khi đó, \(AD = 1,DE = 1,AC = 2,CB = 2\)

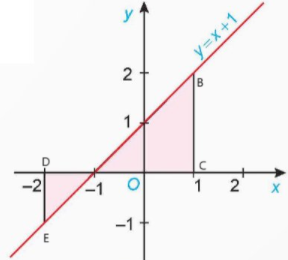
Diện tích S của hình phẳng là:

\(S = {S_{\Delta EAD}} + {S_{\Delta ABC}} = \frac{1}{2}AD.DE + \frac{1}{2}AC.BC = \frac{1}{2}.1.1 + \frac{1}{2}.2.2 = \frac{1}{2} + 2 = \frac{5}{2}\)

b) \(\int\limits_{ - 2}^1 {\left| {f\left( x \right)} \right|dx}  = \int\limits_{ - 2}^1 {\left| {x + 1} \right|dx}  = \int\limits_{ - 2}^{ - 1} {\left| {x + 1} \right|dx}  + \int\limits_{ - 1}^1 {\left| {x + 1} \right|dx =  - \int\limits_{ - 2}^{ - 1} {\left( {x + 1} \right)dx}  + \int\limits_{ - 1}^1 {\left( {x + 1} \right)dx} } \)

\( =  - \left( {\frac{{{x^2}}}{2} + x} \right)\left| \begin{array}{l} - 1\\ - 2\end{array} \right. + \left( {\frac{{{x^2}}}{2} + x} \right)\left| \begin{array}{l}1\\ - 1\end{array} \right. = \left( {\frac{1}{2} + 1 - \frac{1}{2} + 1} \right) - \left( {\frac{{{1^2}}}{2} - 1 - \frac{{{{\left( { - 2} \right)}^2}}}{2} + 2} \right) = 2 + \frac{1}{2} = \frac{5}{2}\)