Bài 3: Đường thẳng đi qua hai điểm
Các câu hỏi tương tự
Mỗi câu sau đây là đúng hay sai ?
a) Có một và chỉ một đường thẳng đi qua hai điểm (phân biệt) cho trước
b) Có đúng ba đường thẳng đi qua ba điểm (phân biệt) cho trước
c) Có đúng 6 đường thẳng đi qua bốn điểm (phân biệt) cho trước
d) Hai đường thẳng phân biệt thì song song với nhau
e) Hai đường thẳng không cắt nhau thì song song với nhau
f) Hai đường thẳng không song song thì cắt nhau
g) Hai đường thẳng không phân biệt thì trùng nhau
h) Ba đường thẳng phân biệt, từng đôi một cắt nhau thì...
Đọc tiếp
Mỗi câu sau đây là đúng hay sai ?
a) Có một và chỉ một đường thẳng đi qua hai điểm (phân biệt) cho trước
b) Có đúng ba đường thẳng đi qua ba điểm (phân biệt) cho trước
c) Có đúng 6 đường thẳng đi qua bốn điểm (phân biệt) cho trước
d) Hai đường thẳng phân biệt thì song song với nhau
e) Hai đường thẳng không cắt nhau thì song song với nhau
f) Hai đường thẳng không song song thì cắt nhau
g) Hai đường thẳng không phân biệt thì trùng nhau
h) Ba đường thẳng phân biệt, từng đôi một cắt nhau thì có đúng 3 giao điểm (phân biệt)
Vẽ hình theo các cách diễn đạt sau :
a) M là giao điểm của hai đường thẳng p và q
b) Hai đường thẳng m và n cắt nhau tại A, đường thẳng p cắt n tại B và cắt m tại C
c) Đường thẳng MN và đường thẳng PQ cắt nhau tại O
Bài 4:Vẽ hình theo cách diễn đạt sau:
a) O là giao điển của hai đường thẳng a và b
b) Vẽ tiếp đường thẳng c cắt tại đường thẳng a tại A và cắt đường thẳng b tại B
c) Vẽ tiếp đường thẳng d cắt đường thẳng a tại M cái đường thẳng b tại M
d) Chỉ ra bộ ba điểm thẳng hàng trong hình vẽ
cho n điểm mà không có ba điểm nào thẳng hàng. Cứ qua hai điểm được 1 đường thẳng.a) biết n =123.Tính số đường thẳng vẽ được.b) biết n=123. Tính số đường thẳng vẽ được khi có đúng 3 điểm thẳng hàng.c) biết số đường thẳng vẽ được là 378. Tính số điểm n
Quan sát hình 21 và cho biết những nhận xét sau đúng hay sai :
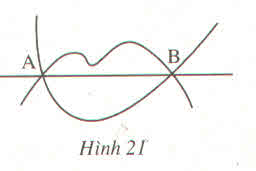
a) Có nhiều đường "không thẳng" đi qua hai điểm A và B
b) Chỉ có một đường thẳng đi qua hai điểm A và B
Cho 3 điểm A,B,C không thẳng hàng.
a)Vẽ đường thẳng đi qua hai điểm A và B
b)Vẽ đường thẳng đi qua hai điểm B và C
c)Vẽ điểm D sao cho A,C,D thẳng hàng
Cho 3 điểm A,B,C không thẳng hàng.
a)Vẽ đường thẳng đi qua hai điểm A và B
b)Vẽ đường thẳng đi qua hai điểm B và C
c)Vẽ điểm D sao cho A,C,D thẳng hàng
Cho 100 điểm phân biệt trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm ta vẽ được một đường thẳng. Hỏi vẽ được tất cả bao nhiêu đường thẳng?
Cho biết có thể vẽ được bao nhiêu đường thẳng (phân biệt) trong mỗi trường hợp sau :
a) Với hai điểm (phân biệt) cho trước
b) Với ba điểm (phân biệt) cho trước và không thẳng hàng
c) Với bốn điểm (phân biệt) cho trước, trong đó không có 3 điểm nào thẳng hàng






