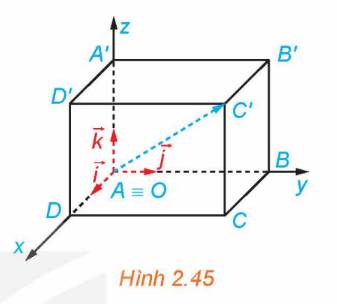
Vì A trùng gốc O nên A(0; 0; 0).
Vì D thuộc tia Ox nên hai vectơ \(\overrightarrow {OD} \) và \(\overrightarrow i \) cùng hướng. Do đó, tồn tại số thực m sao cho \(\overrightarrow {OD} = m\overrightarrow i \). Mà D(2; 0; 0) nên \(m = 2\).
Vì B thuộc tia Oy nên hai vectơ \(\overrightarrow {OB} \) và \(\overrightarrow j \) cùng hướng. Do đó, tồn tại số thực n sao cho \(\overrightarrow {OB} = n\overrightarrow j \). Mà B(0; 4; 0) nên \(n = 4\)
Vì A’ thuộc tia Oz nên hai vectơ \(\overrightarrow {OA'} \) và \(\overrightarrow k \) cùng hướng. Do đó, tồn tại số thực p sao cho \(\overrightarrow {OA'} = p\overrightarrow k \). Mà A’(0; 0; 3) nên \(p = 3\).
Vì ODCB là hình bình hành nên \(\overrightarrow {OC} = \overrightarrow {OD} + \overrightarrow {OB} = m\overrightarrow i + n\overrightarrow j = 2\overrightarrow i + 4\overrightarrow j \). Do đó, C(2; 4; 0).
Vì OA’B’B là hình bình hành nên \(\overrightarrow {OB'} = \overrightarrow {OA'} + \overrightarrow {OB} = p\overrightarrow k + n\overrightarrow j = 3\overrightarrow k + 4\overrightarrow j \). Do đó, B’(0; 4; 3).
Vì OA’D’D là hình bình hành nên \(\overrightarrow {OD'} = \overrightarrow {OA'} + \overrightarrow {OD} = m\overrightarrow i + p\overrightarrow k = 2\overrightarrow i + 3\overrightarrow k \). Do đó, D’(2; 0; 3).
Vì ABCD. A’B’C’D’ là hình hộp chữ nhật nên theo quy tắc hình hộp ta có:
\(\overrightarrow {OC'} = \overrightarrow {OD} + \overrightarrow {OB} + \overrightarrow {OA'} = m\overrightarrow i + n\overrightarrow j + p\overrightarrow k = 2\overrightarrow i + 4\overrightarrow j + 3\overrightarrow k \). Do đó, C’(2; 4; 3).