Question

Trong không gian Oxyz, cho điểm M0 cố định và vectơ \(\overrightarrow{a}\) khác \(\overrightarrow{0}\). Có bao nhiêu đường thẳng d đi qua M₀ và song song hoặc trùng với giá của \(\overrightarrow{a}\).

Answer 1

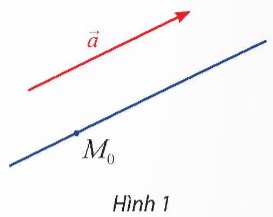
Nếu điểm \({M_0}\) nằm trên giá của vectơ \(\vec a\), thì đường thẳng đó là đường thẳng duy nhất cần tìm.

Nếu điểm \({M_0}\) không nằm trên giá của vectơ \(\vec a\), do trong không gian, qua một điểm không nằm trên một đường thẳng, có duy nhất một đường thẳng đi qua điểm và song song với đường thẳng đó, nên tồn tại duy nhất một đường thẳng đi qua \({M_0}\) và song song với giá của vectơ \(\vec a\).

Như vậy, có duy nhất một đường thẳng \(d\) đi qua \({M_0}\) và song song hoặc trùng với giá của \(\vec a.\)