Question

Trong không gian $O x y z$, cho hai đường thẳng $D$ và $D^{\prime}$ tương ứng có các vectơ chí phương $\vec{u}=(a ; b ; c), \overrightarrow{u^{\prime}}=\left(a^{\prime} ; b^{\prime} ; c^{\prime}\right)($ H.5.34).
a) Hãy tìm mối quan hệ giữa các góc $\left(\mathrm{D}, \mathrm{D}^{\prime}\right)$ và $\left(\vec{u}, \overrightarrow{u^{\prime}}\right)$.
b) Có nhận xét gì về mối quan hệ giữa $\cos \left(\mathrm{D}, \mathrm{D}^{\prime}\right)$ và $\left|\cos \left(\vec{u}, \overrightarrow{u^{\prime}}\right)\right|$ ?

Answer 1

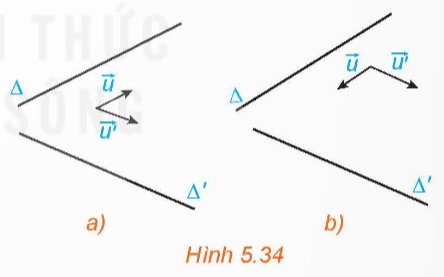
a) Vì \(\overrightarrow u \) và \(\overrightarrow {u'} \) lần lượt là các vectơ chỉ phương của hai đường thẳng \(\Delta \) và \(\Delta '\). Do đó, giá của \(\overrightarrow u \) song song với \(\Delta \), giá của \(\overrightarrow {u'} \) song song với \(\Delta '\). Do đó:

+) \(\left( {\Delta ,\Delta '} \right) = \left( {\overrightarrow u ,\overrightarrow {u'} } \right)\)  nếu \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right) \le {90^o}\)

+) \(\left( {\Delta ,\Delta '} \right) = {180^o} - \left( {\overrightarrow u ,\overrightarrow {u'} } \right)\)  nếu \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right) > {90^o}\)

b) Ta có: \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right|\).