Question

Trong Hình 3.6, hai điểm M, N ứng với hai góc phụ nhau \(\alpha \) và \({90^o} - \alpha \) (\(\widehat {xOM} = \alpha ,\;\;\widehat {xON} = {90^o} - \alpha \)). Chứng mình rằng \(\Delta MOP = \Delta NOQ\). Từ đó nêu mối quan hệ giữa \(\cos \alpha \) và \(\sin \left( {{{90}^o} - \alpha } \right)\).

Answer 1

Tham khảo:

Trường hợp 1:  \(\alpha  = {90^o}\)

Khi đó \({90^o} - \alpha  = {0^o}\)

Tức là M và N lần lượt trùng nhau với B và A.

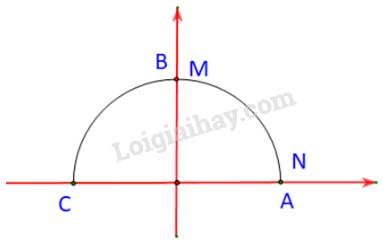
Và  \(\cos \alpha  = 0 = \sin \left( {{{90}^o} - \alpha } \right)\)

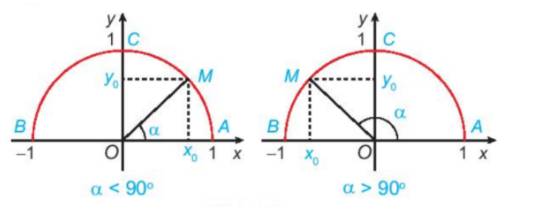
Trường hợp 2: \({0^o} < \alpha  < {90^o} \Rightarrow {0^o} < {90^o} - \alpha  < {90^0}\)

M và N cùng nằm bên trái phải trục tung.

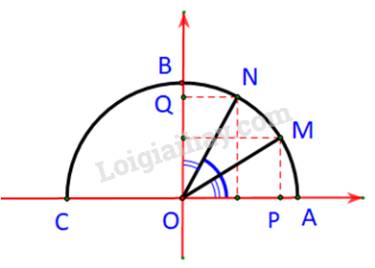
Ta có: \(\alpha  = \widehat {AOM};\;\;{90^o} - \alpha  = \widehat {AON}\)

Dễ thấy: \(\widehat {AON} = {90^o} - \alpha  = {90^o} - \widehat {NOB}\;\;\; \Rightarrow \alpha  = \widehat {NOB}\)

Xét hai tam giác vuông \(NOQ\) và tam giác \(MOP\)  ta có:

\(OM = ON\)

\(\widehat {POM} = \widehat {QON}\)

\(\begin{array}{l} \Rightarrow \Delta NOQ = \Delta MOP\\ \Rightarrow \left\{ \begin{array}{l}OP = OQ\\QN = MP\end{array} \right.\end{array}\)

Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(N\left( {{y_o};{x_0}} \right)\). Nói cách khác:

\(\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha ;\;\;\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha .\)