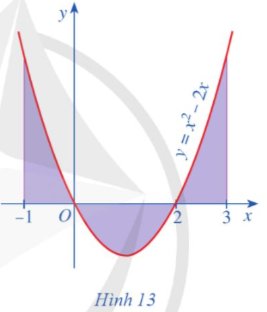
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = {x^2} - 2x\), trục Ox và hai đường thẳng x = -1, x = 3 là:
\(\int\limits_{ - 1}^3 {\left| {{x^2} - 2x} \right|dx} = \int\limits_{ - 1}^0 {\left| {{x^2} - 2x} \right|dx} + \int\limits_0^2 {\left| {{x^2} - 2x} \right|dx} + \int\limits_2^3 {\left| {{x^2} - 2x} \right|dx} \)
\( = \int\limits_{ - 1}^0 {\left( {{x^2} - 2x} \right)dx} + \int\limits_0^2 {\left[ { - \left( {{x^2} - 2x} \right)} \right]dx} + \int\limits_2^3 {\left( {{x^2} - 2x} \right)dx} \)
\( = \left( {\frac{{{x^3}}}{3} - {x^2}} \right)\left| {\begin{array}{*{20}{c}}{^0}\\{_{ - 1}}\end{array}} \right. - \left( {\frac{{{x^3}}}{3} - {x^2}} \right)\left| {\begin{array}{*{20}{c}}{^2}\\{_0}\end{array}} \right. + \left( {\frac{{{x^3}}}{3} - {x^2}} \right)\left| {\begin{array}{*{20}{c}}{^3}\\{_2}\end{array}} \right.\)
\( = \left( {\frac{{{x^3}}}{3} - {x^2}} \right)\left| {\begin{array}{*{20}{c}}{^0}\\{_{ - 1}}\end{array}} \right. - \left( {\frac{{{x^3}}}{3} - {x^2}} \right)\left| {\begin{array}{*{20}{c}}{^2}\\{_0}\end{array}} \right. + \left( {\frac{{{x^3}}}{3} - {x^2}} \right)\left| {\begin{array}{*{20}{c}}{^3}\\{_2}\end{array}} \right.\)
\( = - \left[ {\frac{{{{( - 1)}^3}}}{3} - {{( - 1)}^2}} \right] - \left( {\frac{{{2^3}}}{3} - {2^2}} \right) + \left[ {\left( {\frac{{{3^3}}}{3} - {3^2}} \right) - \left( {\frac{{{2^3}}}{3} - {2^2}} \right)} \right]\)
\( = \frac{4}{3} - \left( { - \frac{4}{3}} \right) + \frac{4}{3} = 4\).