Question

trên mỗi hình 105, 106, 107, 108 có tam giác vuông nào bằng nhau? Vì sao??

Answer 1

Trang bao nhiêu vậy bạn

Answer 2

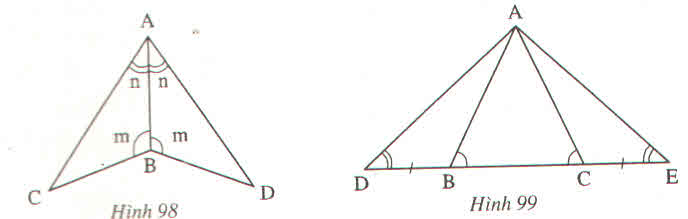
Hình 105

Xét ∆ABH và ∆ACH có:

BH = CH (gt)

AHBˆ = AHCˆ = 90⁰

AH là cạnh chung.

=> ∆ABH = ∆ACH (g.c.g)

Hình 106

Xét ∆DKE và ∆DKF có:

EDKˆ = FDKˆ (giả thiết)

DK là cạnh chung

DKEˆ = DKFˆ = 90⁰

=> ∆DKE = ∆DKF(g.c.g)

Hình 107

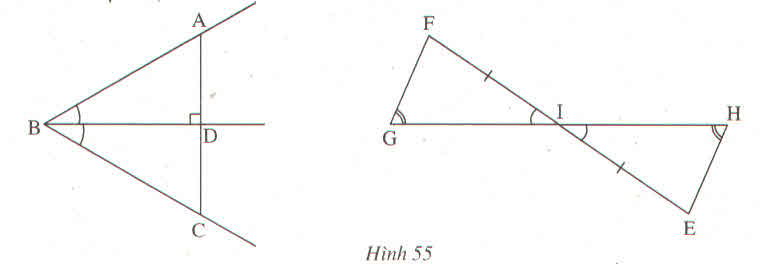
Xét tam giác vuông ∆ABD và tam giác vuông ∆ACD có:

BADˆ = DACˆ (giả thiết)

AD là cạnh chung

=>∆ABD = ∆ACD (cạnh huyền góc nhọn)

Hình 108

Xét tam giác vuông ∆ABD và tam giác vuông ∆ACD có:

BADˆ = DACˆ (giả thiết)

AD là cạnh chung

=>∆ABD = ∆ACD (cạnh huyền góc nhọn)

=>BD = DC , AB = AC (hai cạnh tương ứng)

Xét ∆ABH và ACE có:

ABHˆ = ACEˆ

AB = AC (chứng minh trên)

BACˆ là góc chung

=>∆ABH = ACE (g.c.g)

Xét ∆DBE và ∆ACH có:

EBDˆ = DCHˆ

BD = DC (chứng minh trên)

BDEˆ = CDHˆ

=>∆DBE = ∆ACH (g.c.g)