a,Ta có góc ABC =góc BAC=góc BCA=60•(ABC là Δ đều ) =>BPA=60•
Xét ΔBAQ và ΔBAP có
góc A chung
góc ABQ=góc BPA(60•)
=> ΔBAQ~ΔBPA(g.g)
=>BA/PA=AQ/AB
=>BA2=AP.AQ mà AB=BC
=>BC2=AP.AQ(đpcm )
b,trên đoạn PA lây điểm M sao cho PM=PB thì ta có Tam giác PMB là tam giác đều
vì góc ACB=60=PBM=>ABM=PBC
=> tam giác ABM = tam giác CBP(c.g.c)=> AM=PC
=>PB+PC==PM+AM=PA
a) Ta có: góc ACB= góc APB( 2 góc nội tiếp cùng chắn cung AB)
mà góc ACB= 60 độ ( vì Δ ABC đều)
=> góc APB= 60 độ
Xét Δ QAB và Δ BAP có:
góc APB= góc ABQ= 60 độ
góc BAP là góc chung
=> Δ QAB~Δ BAP(g.g)
=>\(\dfrac{AQ}{AB}\)=\(\dfrac{AB}{AP}\)
=> AB2= AQ.AP
mà AB= BC( vì Δ ABC đều)
=> BC2= AP. AQ( đpcm)
b) Trên đoạn PA lấy điểm M sao cho PM=PB
xét Δ PBM cân tại P( vì PM=PB) có: góc MPB=60 độ
=> Δ PBM là Δ đều
Ta có góc ABM+ góc MBC= góc ABC= 60 độ
góc CBP+ góc MBC= góc MBP= 60 đọ
=> góc ABM= góc CBP
Xét Δ ABM và Δ CBP có:
AB=BC (vì Δ ABC đều)
góc ABM= góc CBP(cmt)
BM=BP( vì Δ MPB đều)
=> Δ ABM=Δ CBP(c-g-c)
=> AM=CP( 2 cạnh tương ứng)
Ta có PB+PC= AM+MP( vì AM=CP; PB=MP)
=> BP+PC=AP(đpcm)
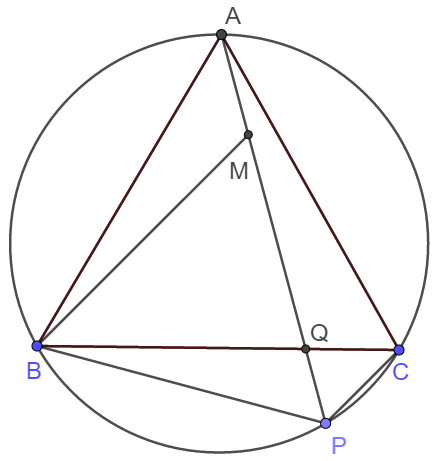
Xét ∆AQB và ∆ABP có
\(\widehat{BPA}=\widehat{ACB}\) (hai góc nội tiếp cùng chắn cung AB)
\(\widehat{BAQ}\) chung
=>∆AQB~∆ABP (g.g)
=> \(\dfrac{AB}{AP}=\dfrac{AQ}{AB}\)
=> \(AB^2\)=AP.AQ
Mà AB=BC (∆ABC đều)
=> \(BC^2\)= AP.AQ (đpcm)
b.Trên đoạn AP lấy điểm M sao cho PM=PB
=>∆PMB đều (∆ cân có 1 góc=60°)
=>\(\widehat{MBP}\)=60°
Mà \(\widehat{ABC}=\)60°
=> \(\widehat{MBP}\)\(=\widehat{ABC}\)
=> \(\widehat{MBP}\)\(-\widehat{MBQ}\)\(=\widehat{ABC}\) \(-\widehat{MBQ}\)
Hay \(\widehat{CBP}=\widehat{ABM}\)
Xét ∆ABM và ∆CBP có
AB= BC (∆ABC đều)
\(\widehat{CBP}=\widehat{ABM}\) (cmt)
BM=BP(cách vẽ)
=>∆ABM=∆CBP(cgc)
=>AM=CP
Ta có AM+PM=AP
=>CP+BP=AP(đpcm)
c. Giả sử\(\dfrac{1}{PQ}=\dfrac{1}{PB}+\dfrac{1}{PC}\Leftrightarrow\dfrac{1}{PQ}=\dfrac{PB+PC}{PB.PC}=\dfrac{AP}{PB.PC}\)
=> PB.PC = AP.PQ
Xét ΔBPQ và ΔAPCcó:
\(\widehat{BPQ}=\widehat{APC}\) (2 góc nội tiếp chắn 2 cung \(\stackrel\frown{AB}=\stackrel\frown{AC}\) )
\(\widehat{PBQ}=\widehat{PAC}\) ( 2 góc nội tiếp cùng chắn \(\stackrel\frown{PC}\))
=>\(\Delta BPQ∽\Delta APC\left(g.g\right)\)
=> \(\dfrac{PB}{AP}=\dfrac{PQ}{PC}\)
=> PB.PC=AP.PQ
Do đó giả sử trên là đúng
Vậy \(\dfrac{1}{PQ}=\dfrac{1}{PB}+\dfrac{1}{PC}\)











