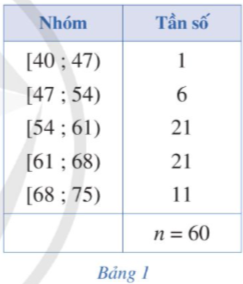
Cỡ mẫu: n = 60.
Ta có \(\frac{n}{4} = \frac{{60}}{4} = 15\), mà 1 + 6 < 15 < 1 + 6 + 21.
Do đó tứ phân vị thứ nhất của mẫu số liệu gốc thuộc nhóm [54;61).
Tứ phân vị thứ nhất của mẫu số liệu là:
\({Q_1} = 54 + \frac{{\frac{{60}}{4} - (1 + 6)}}{{21}}(61 - 54) = \frac{{170}}{3}\).
Ta có \(\frac{{3n}}{4} = \frac{{3.60}}{4} = 45\), mà 1 + 6 + 21 < 45 < 1 + 6 + 21 + 21.
Do đó tứ phân vị thứ ba của mẫu số liệu gốc thuộc nhóm [61;68).
Tứ phân vị thứ ba của mẫu số liệu là:
\({Q_3} = 61 + \frac{{\frac{{3.60}}{4} - (1 + 6 + 21)}}{{21}}(68 - 61) = \frac{{200}}{3}\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
\({\Delta _Q} = {Q_3} - {Q_1} = \frac{{200}}{3} - \frac{{170}}{3} = 10\).