Độ dài cạnh góc vuông của tam giác vuông cân là: \(\frac{5}{\sqrt{2}}\) (cm)
Diện tích tam giác vuông cân là: \(\frac{1}{2}.\left(\frac{5}{\sqrt{2}}\right)^2\) = 6,25 (cm2)
Độ dài cạnh góc vuông của tam giác vuông cân là: \(\frac{5}{\sqrt{2}}\) (cm)
Diện tích tam giác vuông cân là: \(\frac{1}{2}.\left(\frac{5}{\sqrt{2}}\right)^2\) = 6,25 (cm2)
Cho tam giác vuông cân, biết độ dài cạnh huyền là l. Tính diện tích tam giác đó ?
Cho một tam giác vuông cân. Chứng minh rằng tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích của hình vuông dựng trên cạnh huyền (không sử dụng định lí Py-ta-go) ?
Tính diện tích tam giác vuông biết cạnh huyền bằng 13cm, tổng 2 cạnh góc vuông bằng 17cm.
Cho một tam giác vuông. Hãy so sánh tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông với diện tích hình vuông dựng trên cạnh huyền
Gợi ý : Sử dụng định lí Py - ta - go
Câu 7. Một hình thang cân có hai đuong chéo vuông góc với nhau, đo dài đuong chéo bằng 6 cm. Tính diện tích tứ giác có các đinh là trung điểm các cạnh của hình thang cân đó.
cho hình vuông ABCD cạnh 4cm, lấy điểm E thuộc cạnh AB. Biết diện tích tam giác ADE bằng 1:4 diện tích hình vuông ABCD. Tính độ dài AE
Một hình thang cân có hai đường chéo vuông góc với nhau, độ dài đường
chéo bằng 6cm. Tính diện tích tứ giác có các đỉnh là trung điểm của các cạnh
của hình thang cân đó.
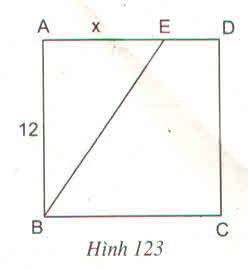
ABCD là một hình vuông cạnh 12 cm, AE = x cm (h.123). Tính x sao cho diện tích tam giác ABE bằng \(\dfrac{1}{3}\) diện tích hình vuông ABCD ?
Cho tam giavs ABC cân tại A, đường cao AM. Gọi I là trung điểm của AC, K là điểm đối xứng với M qua I.
A. Tứ giác AMCK là hình gì? Vì sao
B. Tính diện tích tam giác ABC biết AM=6cm, BC=4cm
C. Tam giác ABC có thêm điều kiện gì thì tứ giác AMCK là hình vuông?