Question

Tính bán kính đường tròn ngoại tiếp tam giác ABC vuông tại A với AB = 5cm, AC = 12cm.

Answer 1

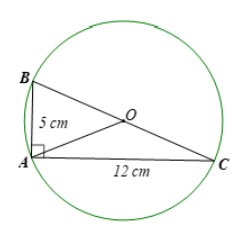
Gọi (O) là đường tròn ngoại tiếp tam giác ABC.

Xét tam giác ABC vuông tại A có:

\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2}(Pytago)\\B{C^2} = {5^2} + {12^2}\\B{C^2} = 169\\BC = 13cm\end{array}\)

Vì ABC vuông tại A nên tâm O của đường tròn ngoại tiếp là trung điểm của cạnh huyền BC (định lý)

Vậy bán kính \(OB = OC = \frac{{BC}}{2} = \frac{{13}}{2}cm.\)